投资组合优化

出自 MBA智库百科(https://wiki.mbalib.com/)

　　投资组合优化是指应用概率论与数理统计、最优化方法以及线性代数等相关数学理论方法，根据既定目标收益和风险容许程度，将投资重新组合，分散风险的过程，它体现了投资者的意愿和投资者所受到的约束，即在一定风险水平下收益最大化或一定收益水平下的风险最小化。

　　相对于一个收益率目标T_t，投资组合在某一时段的收益率R_t可以分成两种情况：

　　或者目标上（V_t），或者目标下（Z_t）

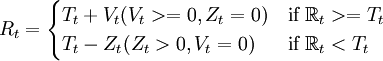
　　投资组合优化的目标是控制下方的风险，即所有的（Z_t）。

　　关于收益率目标T_t的设定：

　　①可以用户给定，如T=20%（年收益率）

　　②可以在行业中同比，如T=行业收益均值

　　③可以在市场中同比，如T=市场收益均值

　　④可以设为自动绝对收益，如T=max{0，行业均值，市场均值}

　　四个最简单的优化目标：

　　1、 极小化最大下方min{(HH_t-RR_t)/HH_t, t=1,2,,N}

　　2、极小化最大下方绝对偏差min{max{Z_t, t=1,2,,N}}

　　3、极小化平均下方绝对偏差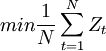

　　4、极小化平均下方绝对偏差平方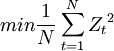

　　基于Konno & Yamazaki(1991)的最小绝对偏差准则和Feinstein & Thepa(1993),及Zenios & Kang(1993)等的下方风险模型，Oberuc(2004)提出了一种直接动态投资组合模型，称作DynaPorte模型:

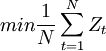　　，AA_jt=A_j + 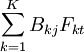(AA–资产配置，F–影响因子)

　　这个模型还包括约束条件：

　　1)资产配置的上限和下限

　　2)使用杠杆的上限和下限

　　3)借款成本

　　4)买卖的佣金

　　这个优化问题的解法是一套线性规划，极小化半绝对偏差，在所有约束条件下。