开映射定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
在泛函分析中，开映射定理是指如果巴拿赫空间之间的连续函数是满射的，那么它就是一个开映射。更加精确地:
如果X和Y是巴拿赫空间，A : X → Y是一个满射的连续线性算子，那么A就是一个开映射（也就是说，如果U是X内的开集，那么A(U)在Y内是开放的）。
该定理的证明用到了贝尔纲定理，X和Y的完备性都是十分重要的。如果仅仅假设X或Y是赋范空间，那么定理的结论就不一定成立。然而，如果X和Y是弗雷歇空间，那么定理的结论仍然成立。
开映射定理有一些重要的推论：
如果A : X → Y是巴拿赫空间X和Y之间的双射连续线性算子，那么反函数A-1 : Y → X也是连续的。
如果A : X → Y是巴拿赫空间X和Y之间的线性算子，且如果对于X内的每一个序列(xn)，只要xn → 0且Axn → y就有y = 0，那么A就是连续的（闭图像定理）。
我们需要证明，如果A : X → Y是巴拿赫空间之间的连续线性满射，那么A就是一个开映射。为此，只需证明A把X内的单位球映射到Y的原点的一个邻域。
设U，V分别为X和Y内的单位球。那么X是单位球的倍数kU的序列的并集，k ∈ N，且由于A是满射，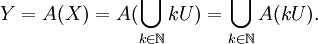 
根据贝尔纲定理，巴拿赫空间Y不能是可数个无处稠密集的并集，故存在k > 0，使得A(kU)的闭包具有非空的内部。因此，存在一个开球B(c, r)，其中心为c，半径r > 0，包含在A(kU)的闭包内。如果v ∈ V，那么c + rv和c位于B(c, r)内，因此是A(kU)的极限点，根据加法的连续性，它们的差rv是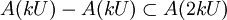
的极限点。根据A的线性，这意味着任何
都位于A(δ1 U)的闭包内，其中δ = r / (2k)。于是可以推出，对于任何
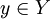和任何ε > 0，都存在某个
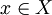，满足：
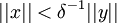且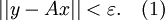 
固定y\in V。根据(1)，存在某个x_1，满足 | | x1 | | 且||y − A x1||<δ / 2。定义序列{xn}如下。假设：
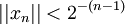且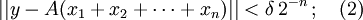 
根据(1)，我们可以选择xn + 1，使得：
且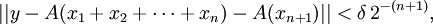 
因此xn + 1满足(2)。设
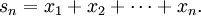
从(2)的第一个不等式可知，{sn}是一个柯西序列，且由于X是完备的，sn收敛于某个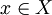。根据(2)，序列Asn}}趋于y，因此根据A的连续性，有Ax=y。而且：
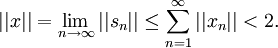
这表明每一个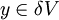
都属于A(2U)，或等价地，X内的单位球的像A(U)包含了Y内的开球(δ / 2)V。因此，A(U)是Y内0的邻域，定理得证。
X 或Y 的局部凸性不是十分重要的，但完备性则是：当X和Y是F空间时，定理仍然成立。更进一步，这个定理可以用以下的方法与贝尔纲定理结合：
设X为F空间，Y为拓扑向量空间。如果A : X → Y是一个连续线性算子，那么要么A(X)是Y内的贫集，要么A(X) = Y。在后一个情况中，A是开映射，Y也是F空间。
更进一步，在这个情况中，如果N是A的核，那么A有一个标准分解，形如下式：
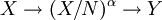
其中X / N是X对闭集N的商空间（也是F空间）。商映射X → X / N是开放的，且映射α是拓扑向量空间的同构。
