古典线性回归模型假定

出自 MBA智库百科(https://wiki.mbalib.com/)

　　古典线性回归模型假定是指高斯提出的10大假定，这些假定被作为大部分计量理论的基石。

　　假定1:线性回归模型。

　　即回归模型在参数上是线性的，这是古典线性回归模型的起点。

　　假定2:在重复抽样中，x值是固定的，非随机的。

　　这个假定的根本意思就是，我们的回归分析是条件回归分析，以给定的解释变量x值为条件。

　　假定3:干扰项具有零均值。即E(ε_i | x_i) = 0。

　　该假定说的就是，没有显性包括在模型中而是包含在\epsilon_i中的因素不会系统地影响y的均值，正的ε_i和负的ε_i会相互抵消，所以，它们对Y的平均影响等于0。

　　假定4:干扰项具有同方差。即Var(ε_i | x_i) = σ²。

　　同方差的意思就是，围绕回归线的变化在不同的x值上是相同的，不会随着x的变化而增加或减少。相反，如果Y总体的条件方差随X而变化，这种情形就称作异方差，即。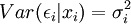

　　假定5:干扰项之间不存在自相关。给定任意两个X值，对应的两个干扰项之问的相关等于0。即，Var(ε_i,ε_j | x_i,x_j)=。。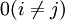

　　假定6:ε_i和X_i之问的协方差等于0。即COV(ε_i,x_i) = E(ε_i,x_i) = 0。

　　假定7:观察值的个数n必须大于要估计的参数的个数。

　　假定8:X值的变化必须足够大。

　　或者说，X的方差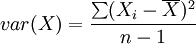

　　必须是一个有限的正值。

　　假定9:回归模型正确设定。

　　假定10:不存在多重共线性。也就是说，在解释变量之间不存在完全的线性关系。这实际上是多元回归中的假定。