全球专业中文经管百科，由121,994位网友共同编写而成，共计436,017个条目

查看

工具箱▼

变额年金法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

1 什么是变额年金法
2 变额年金法的分类及计算[1]
3 相关条目
4 参考文献

什么是变额年金法

　　变额年金法是每期支付的租金金额不相等的租金支付方式。

变额年金法的分类及计算^[1]

　　变额年金法分为等差变额年金法和等比变额年金法。

　　①等差变额年金法。

　　在这种方法下，每期租金都比前一期增加一个常数d。其公式是：

　　 $R_1=\frac{i(1+i)^n}{(1+i)^n-1}[P+\frac{d}{i}(n- \frac{(1+i)^n-1}{i(1+i)^n})]-nd$

　　式中： $R 1$ 真为第一期期末支付的租金；d为常数。

　　根据定义： $R 2 = R 1 + d$

　　 $R 3 = R 1 + 2 d$

　　……

　　 $R n = R 1 + (n - 1) d$

　　将上面 $R 1$ , $R 2$ , $R 3$ …… $R n$ 的内容代入

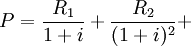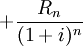　　 $P= \frac{R_1}{1+i}+ \frac{R_2}{(1+i)^2}+$ …… $+ \frac{R_n}{(1+i)^n}$ 得：

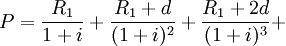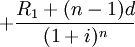
　　 $P= \frac{R_1}{1+i}+ \frac{R_1+d}{(1+i)^2}+ \frac{R_1+2d}{(1+i)^3}+$ …… $+ \frac{R_1+(n-1)d}{(1+i)^n}$

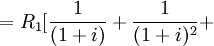　　 $= R_1[\frac{1}{(1+i)}+ \frac{1}{(1+i)^2}+$ …… $+ \frac{1}{(1+i)^n}]+d[\frac{1}{(1+i)^2}+ \frac{2}{(1+i)^3}+$ …… $+ \frac{(n-1)}{(1+i)^n}]$

　　 $= R_1 \frac{(1+i)^n-1}{i(1+i)^n}+nd \times \frac{(1+i)^n-1}{i(1+i)^n}-d[\frac{n}{1+i}+ \frac{n-1}{(1+i)^2}+$ …… $+ \frac{1}{(1+i)^n}]$

　　所以： $R_1= \frac{i(1+i)^n}{(1+i)^n-1}[P+ \frac{d}{i}(n- \frac{i(1+i)^n}{(1+i)^n-1})]-nd$

　　如果d > 0，则后一期租金比前一期租金增加一个正数，称为等差递增变额年金法。

　　如果d < 0，则后一期租金比前一期租金增加一个负数，称为等差递减变额年金法。

　　如果d＝0，则为等额年金法，因此，等额年金法是变额年金法的特例。

　　②等比变额年金法。

　　在这种方法下，每期租金与前一期租金的比值总是一个常数q。公式如下：

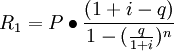
　　 $R_1=P \bullet \frac{(1+i-q)}{1-(\frac{q}{1+i})^n}$

　　式中： $R 1$ 为第一期期末支付的租金额；q为常数。

　　公式可推导如下：

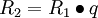
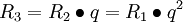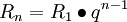
　　 $R_2=R_1 \bullet q$ $R_3=R_2 \bullet q=R_1 \bullet q^2$ …… $R_n=R_1 \bullet q^{n-1}$

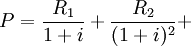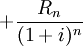　　把上式代入等式 $P= \frac{R_1}{1+i}+ \frac{R_2}{(1+i)^2}+$ …… $+ \frac{R_n}{(1+i)^n}$ 得：

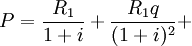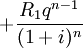
　　 $P=\frac{R_1}{1+i}+ \frac{R_1q}{(1+i)^2}+$ …… $+ \frac{R_1q^{n-1}}{(1+i)^n}$

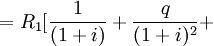　　 $=R_1[\frac{1}{(1+i)}+ \frac{q}{(1+i)^2}+$ …… $+ \frac{q^{n-1}}{(1+i)^n}]$

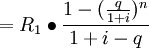
　　 $=R_1 \bullet \frac{1- (\frac{q}{1+i})^n}{1+i-q}$

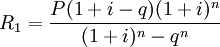
　　所以， $R_1=\frac{P(1+i-q)}{1- (\frac{q}{1+i})^n}$ 或者 $R_1=\frac{P(1+i-q)(1+i)^n}{(1+i)^n - q^n}$

　　如果q > 1，则为等比递增变额年金法。

　　如果q < 1，则为等比递减变额年金法。

　　如果q = 1，则为等额年金法。

　　由此我们可以看出，使用变额年金法，每次支付租金的金额不同，有时递增、有时递减；此法符合收益与成本相配比的原则；d与q的大小难以确定，而且d、q越大，租金增额越多。

相关条目

参考文献

↑ 张素琴,吴祖明,张功富等.现代金融学概论.首都经济贸易大学出版社,1997年08月第1版

来自"https://wiki.mbalib.com/wiki/%E5%8F%98%E9%A2%9D%E5%B9%B4%E9%87%91%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

KAER,可恨密码记不住,方小莉.

页面分类: 财务管理方法 | 年金

评论(共0条)

提示:评论内容为网友针对条目"变额年金法"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号