乘数—加速原理相互作用理论
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
乘数-加速原理相互作用理论:是把投资水平和国民收入变化率联系起来解释国民收入周期波动的一种理论,是最具影响的内生经济周期理论。
乘数一加速原理相互作用理论是凯恩斯主义者提出的 。凯恩斯主义认为引起经济周期的因素是总需求,在总需求中起决定作用的是投资。这种理论正是把乘数原理和加速原理结合起来说明投资如何自发地引起周期性经济波动。
经济学家认为,经济中之所以会发生周期性波动其根源正在于乘数原理与加速原理的相互作用。具体来说,乘数一加速原理所说明的是:
第一,在经济中投资、国内生产总值、消费相互影响,相互调节。如果政府支出为既定的(即政府不干预经济),只靠经济本身的力量自发调节,那么,就会形成经济周期。经济周期中各阶段的出现,正是乘数与加速原理相互作用的结果。而在这种自发调节中,投资是关键的,经济周期主要是投资引起的。
第二,乘数与加速原理相互作用引起经济周期的具体过程是,投资增加通过乘数效应引起国内生产总值的更大增加,国内生产总值的更大增加又通过加速效应引起投资的更大增加,这样,经济就会出现繁荣。然而,国内生产总值达到一定水平后由于社会需求与资源的限制无法再增加,这时就会由于加速原理的作用使投资减少,投资的减少又会由于乘数的作用使国内生产总值继续减少。这两者的共同作用又使经济进入衰退。衰退持续一定时期后由于固定资产更新,即大规模的机器设备更新又使投资增加,国内生产总值再增加,从而经济进入另一次繁荣。正是由于乘数与加速原理的共同作用,经济中就形成了由繁荣到衰退,又由衰退到繁荣的周期性运动。
第三,政府可以通过干预经济的政策来减轻、甚至消除经济周期的波动。
乘数-加速原理表明国内生产总值的变化会通过加速数对投资产生加速作用,而投资的变化又会通过投资乘数使国内生产总值成倍变化,加速数和投资乘数的这种交织作用便导致国内生产总值周而复始的上下波动。
在国民经济中,投资与国民收入是相互影响的。乘数原理说明了投资变动对国民收入变动的影响,而加速原理要说明国民收入变动对投资变动的影响。
所以说,加速原理是论证投资取决于国民收入(或产量)变动率的理论。
其公式如下:
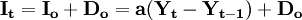 公式(1)
公式(1)
在上式中,
- Io取决于加速系数a和本期收入Yt与上期收入Yt − 1的差异。
加速系数(a)指产量增加一定量所需要增加的净投资量,即净投资量与产量增加一定量所需要增加的技术水平。
其公式:
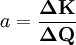 公式(2)
公式(2)
- ΔK :所需要增加的投资
- ΔQ :每增加一单位产量
例如,如果在一定的生产技术水平之下,增加100万元的产量需要增加的净投资为200万元,则加速系数为2。
与加速系数相关的另一个概念是资本—产量比率,即生产一单位产量所需要的资本量,或者资本量与产量之比。在技术不变的条件下,加速系数与资本—产量比率的数值是相同的。
乘数—加速模型就是把这两种原理结合起来,以说明经济周期的原因。这一模型的表述为这样一个公式:
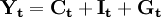 公式(1)
公式(1)
上式中
- Yt为现期收入,
- Ct为现期消费,
- It为现期投资,
- Gt为现期政府支出。
这个公式说明了,根据凯恩斯主义的国民收入决定理论,现期收入等于现期消费、现期投资与现期政府支出之和(不考虑开放经济中的净出口)。
现期消费取决于边际消费倾向c和前期收入Yt − 1;
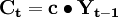 公式(2)
公式(2)
现期投资取决于加速系数(a)和消费的变动(Ct − Ct − 1);
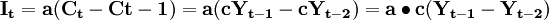 公式(3)
公式(3)
(3)式说明了在考虑消费时,投资最终仍取决于收入的变动,即加速原理说明的关系。
设现期政府支出为即定的,即:
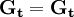 公式(4)
公式(4)
把(2)、(3)、(4)式代入(1)式则得出:
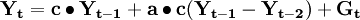 公式(5)
公式(5)
可以通过对c,a,Gt,进行设值计算
据此可得到乘数—加速模型的完整含义
(1)在经济中投资、国民收入、消费相互影响,相互调节。如果政府支出为既定(即政府不干预经济),只靠经济本身的力量自发调节,那么就会形成经济周期。周期中各阶段的出现,正是乘数与加速原理相互作用的结果。而在这种自发调节中,投资是关键的,经济周期主要是投资引起的。
(2)乘数与加速原理相互作用引起经济周期的具体过程是:投资增加引起产量的更大增加,产量的更大增加又引起投资的更大增加,这样,经济就会出现繁荣。然而,产量达到一定水平后由于社会需求与资源的限制无法再增加,这时就会由于加速原理的作用使投资减少,投资的减少又会由于乘数的作用使产量继续减少,这两者的共同作用又会使经济进入萧条。萧条持续一定时期后由于产量回升又使投资增加、产量再增加,从而经济进入另一次繁荣。正是由于乘数与加速原理的共同作用,经济中就形成了由繁荣到萧条,又由萧条到繁荣的周期性运动过程。
(3)政府可以通过干预经济的政策来影响经济周期的波动。即利用政府的干预(比如政府投资变动)就可以影响减轻经济周期的破坏性,甚至消除周期,实现国民经济持续稳定的增长。








必考