標準偏差
出自 MBA智库百科(https://wiki.mbalib.com/)
標準偏差(Std Dev,Standard Deviation)
目錄 |
標準偏差(也稱標準離差或均方根差)是反映一組測量數據離散程度的統計指標。是指統計結果在某一個時段內誤差上下波動的幅度。是正態分佈的重要參數之一。是測量變動的統計測演算法。它通常不用作獨立的指標而與其它指標配合使用。
標準偏差在誤差理論、質量管理、計量型抽樣檢驗等領域中均得到了廣泛的應用。因此, 標準偏差的計算十分重要, 它的準確與否對器具的不確定度、測量的不確定度以及所接收產品的質量有重要影響。然而在對標準偏差的計算中, 不少人不論測量次數多少, 均按貝塞爾公式計算。
數學表達式:
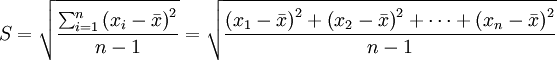
- S-標準偏差(%)
- n-試樣總數或測量次數,一般n值不應少於20-30個
- i-物料中某成分的各次測量值,1~n;
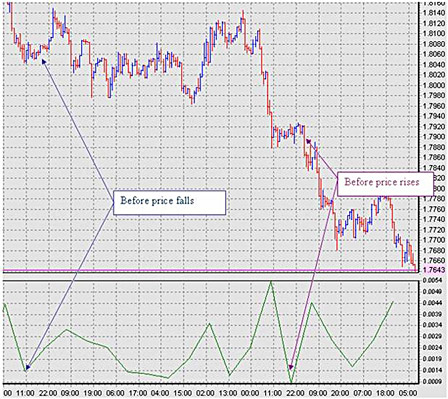
- 在價格變化劇烈時,該指標值通常很高。
- 如果價格保持平穩,這個指標值不高。
- 在價格發生劇烈的上漲/下降之前,該指標值總是很低。
標準偏差的計算步驟是:
步驟一、(每個樣本數據 - 樣本全部數據之平均值)2。
步驟二、把步驟一所得的各個數值相加。
步驟三、把步驟二的結果除以 (n - 1)(“n”指樣本數目)。
步驟四、從步驟三所得的數值之平方根就是抽樣的標準偏差。
六個計算標準偏差的公式[1]
設對真值為X的某量進行一組等精度測量, 其測得值為l1、l2、……ln。令測得值l與該量真值X之差為真差占σ, 則有 σ1 = li − X
σ2 = l2 − X
……
σn = ln − X
我們定義標準偏差σ為
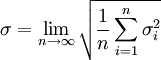
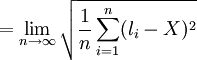 (1)
(1)
由於真值X都是不可知的, 因此真差σ占也就無法求得, 故式只有理論意義而無實用價值。
由於真值是不可知的, 在實際應用中, 我們常用n次測量的算術平均值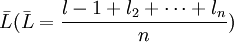 來代表真值。理論上也證明, 隨著測量次數的增多, 算術平均值最接近真值, 當
來代表真值。理論上也證明, 隨著測量次數的增多, 算術平均值最接近真值, 當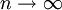 時, 算術平均值就是真值。
時, 算術平均值就是真值。
於是我們用測得值li與算術平均值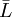 之差——剩餘誤差(也叫殘差)Vi來代替真差σ , 即
之差——剩餘誤差(也叫殘差)Vi來代替真差σ , 即
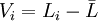
設一組等精度測量值為l1、l2、……ln
則 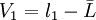
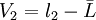
……
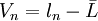
通過數學推導可得真差σ與剩餘誤差V的關係為
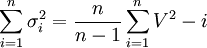
將上式代入式(1)有
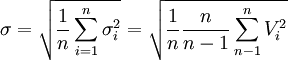
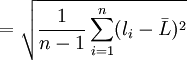 (2)
(2)
式(2)就是著名的貝塞爾公式(Bessel)。
它用於有限次測量次數時標準偏差的計算。由於當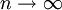 時,
時,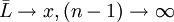 ,可見貝塞爾公式與σ的定義式(1)是完全一致的。
,可見貝塞爾公式與σ的定義式(1)是完全一致的。
應該指出, 在n有限時, 用貝塞爾公式所得到的是標準偏差σ的一個估計值。它不是總體標準偏差σ。因此, 我們稱式(2)為標準偏差σ的常用估計。為了強調這一點, 我們將σ的估計值用“S ” 表示。於是, 將式(2)改寫為
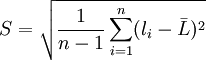 (2')
(2')
在求S時, 為免去求算術平均值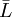 的麻煩, 經數學推導(過程從略)有
的麻煩, 經數學推導(過程從略)有
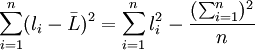
於是, 式(2')可寫為
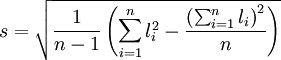 (2")
(2")
按式(2")求S時, 只需求出各測得值的平方和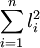 和各測得值之和的平方藝
和各測得值之和的平方藝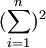 , 即可。
, 即可。
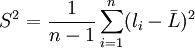
數學上已經證明S2是總體方差σ2的無偏估計。即在大量重覆試驗中, S2圍繞σ2散佈, 它們之間沒有系統誤差。而式(2')在n有限時,S並不是總體標準偏差σ的無偏估計, 也就是說S和σ之間存在系統誤差。概率統計告訴我們, 對於服從正態分佈的正態總體, 總體標準偏差σ的無偏估計值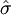 為
為
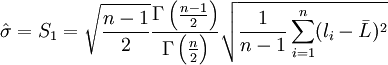 (3)
(3)
令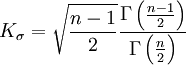
則 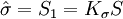
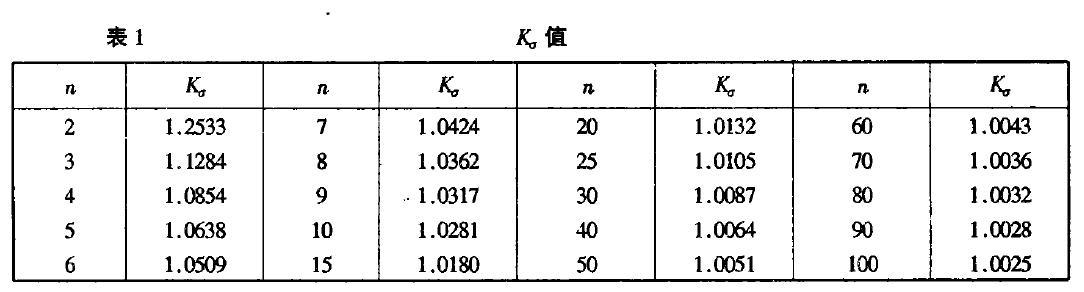
即S1和S僅相差一個繫數Kσ,Kσ是與樣本個數測量次數有關的一個繫數, Kσ值見表。
計算Kσ時用到
Γ(n + 1) = nΓ(n)
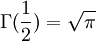
Γ(1) = 1
由表1知, 當n>30時, 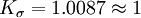 。因此, 當n>30時, 式(3')和式(2')之間的差異可略而不計。在n=30~50時, 最宜用貝塞爾公式求標準偏差。當n<10時, 由於Kσ值的影響已不可忽略, 宜用式(3'), 求標準偏差。這時再用貝塞爾公式顯然是不妥的。
。因此, 當n>30時, 式(3')和式(2')之間的差異可略而不計。在n=30~50時, 最宜用貝塞爾公式求標準偏差。當n<10時, 由於Kσ值的影響已不可忽略, 宜用式(3'), 求標準偏差。這時再用貝塞爾公式顯然是不妥的。
將σ的定義式(1)中的真值X用算術平均值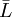 代替且當n有限時就得到
代替且當n有限時就得到
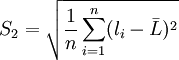
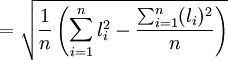 (4)
(4)
式(4)適用於n>50時的情況, 當n>50時,n和(n-1)對計算結果的影響就很小了。
2.5標準偏差σ的極差估計由於以上幾個標準偏差的計算公式計算量較大, 不宜現場採用, 而極差估計的方法則有運算簡便, 計算量小宜於現場採用的特點。
極差用"R"表示。所謂極差就是從正態總體中隨機抽取的n個樣本測得值中的最大值與最小值之差。
若對某量作次等精度測量測得l1、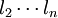 ,且它們服從正態分佈, 則
,且它們服從正態分佈, 則
R = lmax − lmin
概率統計告訴我們用極差來估計總體標準偏差的計算公式為
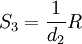 (5)
(5)
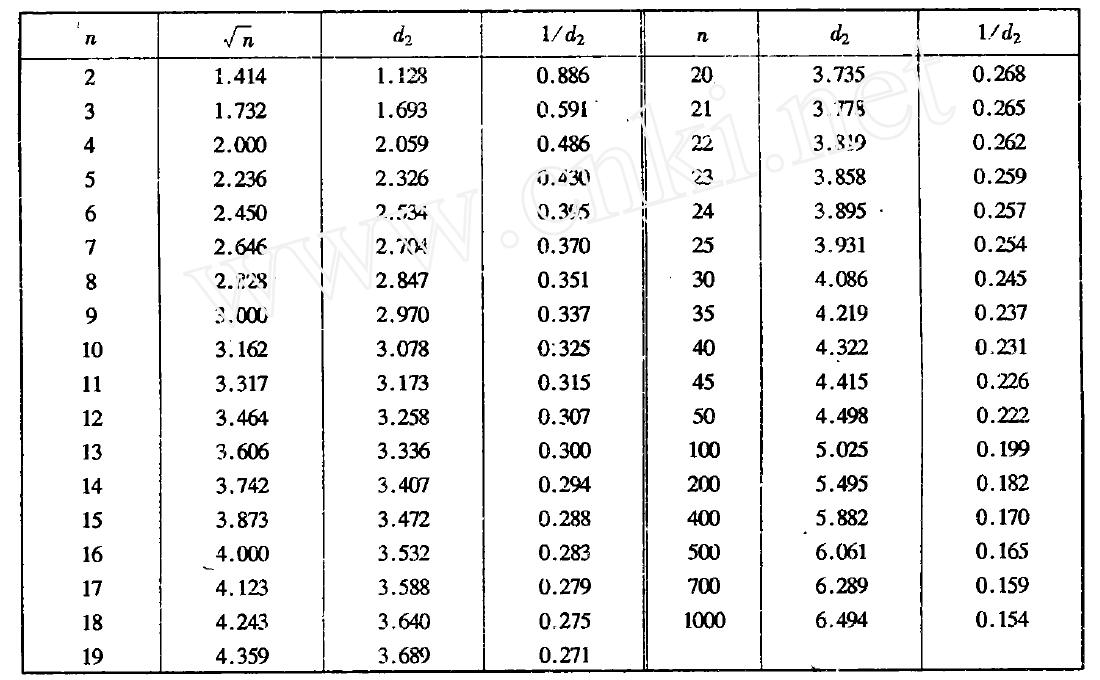
S3稱為標準偏差σ的無偏極差估計, d2為與樣本個數n(測得值個數)有關的無偏極差繫數, 其值見表2
由表2知, 當n≤15時,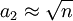 , 因此, 標準偏差σ更粗略的估計值為
, 因此, 標準偏差σ更粗略的估計值為
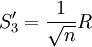 (5')
(5')
還可以看出, 當200≤n≤1000時,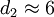 因而又有
因而又有
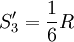 (5")
(5")
顯然, 不需查表利用式(5')和(5")了即可對標準偏差值作出快速估計, 用以對用貝塞爾公式及其他公式的計算結果進行校核。
應指出,式(5)的準確度比用其他公式的準確度要低, 但當5≤n≤15時,式(5)不僅大大提高了計算速度, 而且還頗為準確。當n>10時, 由於捨去數據信息較多, 因此誤差較大, 為了提高準確度, 這時應將測得值分成四個或五個一組, 先求出各組的極差R1、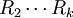 , 再由各組極差求出極差平均值
, 再由各組極差求出極差平均值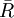 。
。
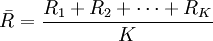
極差平均值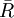 和總體標準偏差的關係為
和總體標準偏差的關係為
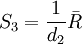
需指出, 此時d2大小要用每組的數據個數n而不是用數據總數N(=nK)去查表2。再則, 分組時一定要按測得值的先後順序排列,不能打亂或顛倒。
平均誤差的定義為
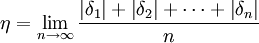
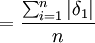
誤差理論給出
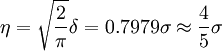 (A)
(A)
可以證明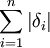 與
與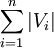 的關係為
的關係為
(證明從略)
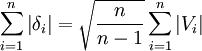
於是 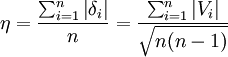 (B)
(B)
由式(A)和式(B)得
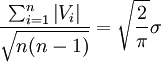
從而有
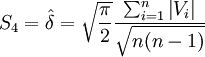
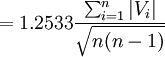
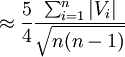
式(6)就是佩特斯(C.A.F.Peters.1856)公式。用該公式估計δ值, 由於\right|V\right|不需平方,故計算較為簡便。但該式的準確度不如貝塞爾公式。該式使用條件與貝塞爾公式相似。
標準偏差的應用實例[1]
對標稱值Ra = 0.160 < math > μm < math > 的一塊粗糙度樣塊進行檢定, 順次測得以下15個數據:1.45,1.65,1.60,1.67,1.52,1.46,1.72,1.69,1.77,1.64,4.56,1.50,1.64,1.74和1.63μm, 試求該樣塊Rn的平均值和標準偏差並判斷其合格否。
解:1)先求平均值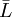
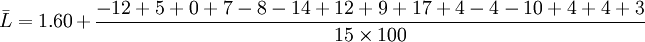
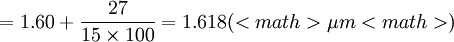
2)再求標準偏差S
若用無偏極差估計公式式(5)計算, 首先將測得的, 15個數據按原順序分為三組, 每組五個, 見表3。
表3
組號 l_1 l_5 R 1 1.48 1.65 1.60 1.67 1.52 0.19 2 1.46 1.72 1.69 1.77 1.64 0.31 3 1.56 1.50 1.64 1.74 1.63 0.24
因每組為5個數據, 按n=5由表2查得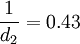
故
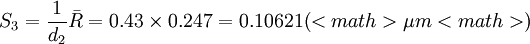
若按常用估計即貝塞爾公式式(2') , 則
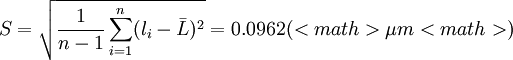
若按無偏估計公式即式(3')計算, 因n=15,由表1查得Kδ = 1.018, 則
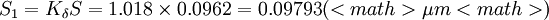
若按最大似然估計公式即式(4')計算, 則
![S_2=\sqrt{\frac{1}{n}\left[\sum^n_{i=1}l^2_i-\frac{(\sum^n_{i=1}l_i)^2}{n}\right]}](/w/images/math/3/a/1/3a1618dde60cf9bc00acc01adfd5ec7f.png)
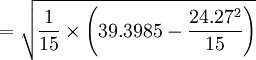
= 0.09296( < math > μm < math > )
若按平均誤差估計公式即式(6), 則
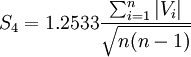
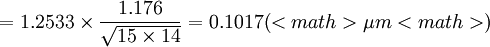
現在用式(5')對以上計算進行校核
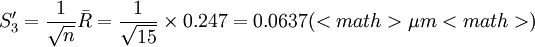
可見以上算得的S、S1、S2、S3和S4沒有粗大誤差。
由以上計算結果可知0.09296<0.0962<0.0979<0.1017<0.1062
即 S2 < S < S1 < S4 < S3
可見, 最大似然估計值最小, 常用估計值S稍大, 無偏估計值S1又大, 平均誤差估計值S4再大, 極差估計值S3最大。縱觀這幾個值, 它們相當接近, 最大差值僅為0.01324μm。從理論上講, 用無偏估計值和常用估計比較合適, 在本例中, 它們僅相差0.0017μm。可以相信, 隨著的增大, S、S1、S2、S3和S4之間的差別會越來越小。
就本例而言, 無偏極差估計值S3和無偏估計值S1僅相差0.0083μm, 這說明無偏極差估計是既可以保證一定准確度計算又簡便的一種好方法。
JJG102-89《錶面粗糙度比較樣塊》規定Ra的平均值對其標稱值的偏離不應超過+12%~17%, 標準偏差應在標稱值的4%~12%之間。已得本樣塊二產, 產均在規定範圍之內, 故該樣塊合格。
產均在規定範圍之內, 故該樣塊合格。
標準差(Standard Deviation)各數據偏離平均數的距離(離均差)的平均數,它是離差平方和平均後的方根。用σ表示。因此,標準差也是一種平均數。標準差是方差的算術平方根。 標準差能反映一個數據集的離散程度。平均數相同的,標準差未必相同。
例如,A、B兩組各有6位學生參加同一次語文測驗,A組的分數為95、85、75、65、55、45,B組的分數為73、72、71、69、68、67。這兩組的平均數都是70,但A組的標準差為17.08分,B組的標準差為2.16分,說明A組學生之間的差距要比B組學生之間的差距大得多。
標準偏差(Std Dev,Standard Deviation) - 統計學名詞。一種量度數據分佈的分散程度之標準,用以衡量數據值偏離算術平均值的程度。標準偏差越小,這些值偏離平均值就越少,反之亦然。標準偏差的大小可通過標準偏差與平均值的倍率關係來衡量。
評論(共10條)
可以請教一題嗎? 甲組:2.9 2.9 3.0 3.1 3.1 乙組:2.8 3.0 3.0 3.0 3.2 我計算出平均值各是3.0 平均偏差 D甲:0.08 / D乙:0.08 可是標準偏差S是怎麼算出來呢?
可以請教一題嗎? 甲組:2.9 2.9 3.0 3.1 3.1 乙組:2.8 3.0 3.0 3.0 3.2 我計算出平均值各是3.0 平均偏差 D甲:0.08 / D乙:0.08 可是標準偏差S是怎麼算出來呢?
按上面的計算步驟來算,甲:0.1;乙:0.141。不知道對不對
按上面的計算步驟來算,甲:0.1;乙:0.141。不知道對不對
我也認為甲是0.1,乙是0.14
所以意思是「標準偏差=標準差」嗎?
看不太懂
按樓主的意思應該是這樣








謝謝了,非常有用。正不知道怎麼辦呢,萬分感謝