整數規劃
出自 MBA智库百科(https://wiki.mbalib.com/)
整數規劃(integer programming)
目錄 |
整數規劃是指一類要求問題中的全部或一部分變數為整數的數學規劃。是近三十年來發展起來的、規劃論的一個分支. 整數規劃問題是要求決策變數取整數值的線性規劃或非線性規劃問題。
一般認為非線性的整數規劃可分成線性部分和整數部分,因此常常把整數規劃作為線性規劃的特殊部分。線上性規劃問題中,有些最優解可能是分數或小數,但對於某些具體問題,常要求解答必須是整數。例如,所求解是機器的台數,工作的人數或裝貨的車數等。為了滿足整數的要求,初看起來似乎只要把已得的非整數解舍入化整就可以了。實際上化整後的數不見得是可行解和最優解,所以應該有特殊的方法來求解整數規劃。在整數規劃中,如果所有變數都限製為整數,則稱為純整數規劃;如果僅一部分變數限製為整數,則稱為混合整數規劃。整數規劃的一種特殊情形是01規劃,它的變數僅限於0或1。
整數規劃是從1958年由R.E.戈莫里提出割平面法之後形成獨立分支的 ,30多年來發展出很多方法解決各種問題。解整數規劃最典型的做法是逐步生成一個相關的問題,稱它是原問題的衍生問題。對每個衍生問題又伴隨一個比它更易於求解的鬆弛問題(衍生問題稱為鬆弛問題的源問題)。通過鬆弛問題的解來確定它的源問題的歸宿,即源問題應被捨棄,還是再生成一個或多個它本身的衍生問題來替代它。隨即 ,再選擇一個尚未被捨棄的或替代的原問題的衍生問題,重覆以上步驟直至不再剩有未解決的衍生問題為止。目前比較成功又流行的方法是分枝定界法和割平面法,它們都是在上述框架下形成的。
0—1規劃在整數規劃中占有重要地位,一方面因為許多實際問題,例如指派問題、選地問題、送貨問題都可歸結為此類規劃,另一方面任何有界變數的整數規劃都與0—1規劃等價,用0—1規劃方法還可以把多種非線性規劃問題表示成整數規劃問題,所以不少人致力於這個方向的研究。求解0—1規劃的常用方法是分枝定界法,對各種特殊問題還有一些特殊方法,例如求解指派問題用匈牙利方法就比較方便。
整數規劃與組合最優化從廣泛的意義上說,兩者的領域是一致的,都是在有限個可供選擇的方案中,尋找滿足一定標準的最好方案。有許多典型的問題反映整數規劃的廣泛背景。例如,背袋(或裝載)問題、固定費用問題、和睦探險隊問題(組合學的對集問題)、有效探險隊問題(組合學的覆蓋問題)、送貨問題等。因此整數規劃的應用範圍也是極其廣泛的。它不僅在工業和工程設計和科學研究方面有許多應用,而且在電腦設計、系統可靠性、編碼和經濟分析等方面也有新的應用。
整數規劃又分為:
1、純整數規劃:所有決策變數均要求為整數的整數規劃
2、混合整數規劃:部分決策變數均要求為整數的整數規劃
3、純0-1整數規劃:所有決策變數均要求為0-1的整數規劃
4、混合0-1規劃:部分決策變數均要求為0-1的整數規劃
整數規劃與線性規劃不同這處只在於增加了整數約束。不考慮整數約束所得到的線性規劃稱為整數規劃的線性鬆弛模型。
在現實生活中,決策變數代表產品的件數、個數、台數、箱數、艘數、輛數等等,則變數就只能取整數值. 如截料模型實際上就是一個整數規劃模型,該例的決策變數代表所截鋼管的根數,顯然只能取整數值。因而整數規劃模型也有著廣泛的應用領域,從 以下的幾個例子中更可以窺其一斑。
[例1] 某廠在一計劃期內擬生產甲、乙兩種大型設備. 該廠有充分的生產能力來加工製造這兩種設備的全部零件,所需原材料和能源也可滿足供應,但A、B兩種緊缺物資的供應受到嚴格限制,每台設備所需原材料如下 表所示. 問該廠在本計劃期內應安排生產甲、乙設備多少台,才能使利潤達到最大?
原料設備 甲 乙 可供資源數量 A(噸) 1 1 6 B(千克) 5 9 45 每台單位利潤(萬元) 5 6
解: 設x1,x2分別為該計劃期內生產甲、乙設備的台數,Z為生產這兩種設備可獲得的總利潤.顯然x1,x2都須是非負整數,因此它是一個(純)整數規劃問題,其數學模型為:
max Z = 5x1 + 8x2
s.t. x1 + x26
5x1 + 9x245
x1,x2 0
x1,x2為整數
[例2] (投資決策模型)設有n個投資項目,其中第j個項目需要資金aj萬元,將來可獲利潤cj萬元。若現有資金總額為b萬元,則應選擇那些投資項目,才能獲利最大? 解: 設:
這裡j=1,2,…n設Z為可獲得的總利潤(萬元),則該問題的數學模型為:
max 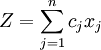
s.t. 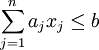
xj=0 or 1(j = 1,2,Λ,n)
[例3] (物資調撥模型)某廠擬用a元資金生產m種設備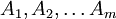 其中設備Ai單位成本為pi (i=1,2,…,m)。預計將一臺設備Ai在Bj處銷售可獲利xij元,則應如何調撥這些設備,才能使預計總利潤為最大?
其中設備Ai單位成本為pi (i=1,2,…,m)。預計將一臺設備Ai在Bj處銷售可獲利xij元,則應如何調撥這些設備,才能使預計總利潤為最大?
解 設yi為生產設備Ai的台數,xij為將設備Ai調撥到Bj處銷售的台數,Z為預計總利潤(元). 則該問題的數學模型為:
max 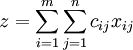
s.t. 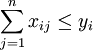 (i = 1,2,Λ,m)
(i = 1,2,Λ,m)
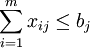 (j = 1,2,Λ,n)
(j = 1,2,Λ,n)
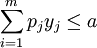
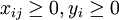
xij,yi均為整數
[例4] (選址問題)某種商品有n個銷地,各銷地每月的需求量分別為bj噸(j=1,2,…,n).。現擬在m個地點中選址建廠,來生產這種產品以滿足供應,且規 定一個地址最多只能建一個工廠。若選址i建廠,將來生產能力每月為ai噸,生產成本每月為di元(i=1,2,…,m). 已知從i至銷地j的運價為cij元/噸. 應如何選擇廠址和安排調運,能使總的最少?
解 設每月從廠址i至銷地j的運量為x_{ij}噸,z為每月的總費用(元),
則該問題的數學模型為:
min 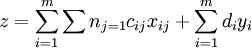
s.t. 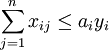 (i = 1,2,Λ,m)
(i = 1,2,Λ,m)
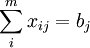 (j = 1,2,Λ,m)
(j = 1,2,Λ,m)
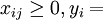 0 or 1
0 or 1
求解整數規劃的一種自然的想法是,能否用整數規劃的線性鬆弛模型的最優解經過四捨五入得到整數規劃的最優解呢?回答是否定的,因為這樣四捨五入的結果甚至不是可行解。
整數規劃比通常的線性規劃更加難以求解,迄今求解整數規劃其基本求解思路都是按一定的搜索規則,在整數規劃的線性鬆弛模型的可行域內尋找出整數最優解(或確認無整數最優解),因此求整數規劃的解需要更多的時間,現通用的解法,主要有分支定界法、割平面法和窮舉法等。
案例一:整數規劃在多方案選擇中的應用[1]
在經濟建設中,企業總有各種各樣的投資機會,每一種投資機會又有多種的投資方式,每一種投資方式都稱為一個投資方案,所以經濟建設中企業總有多方案可供選擇,同時需要大量的資源,而資源是有限的,因此企業要根據有限的資源確定投資方案的順序,使有限的資源取得最大的效益。即經濟建設中企業要進行多方案的最佳選擇。
一、多方案選擇的傳統方法
多方案的選擇,必須明確各方案之間的關係,方案之間關係不同,其選擇的方法也不同。方案之間的關係可以概括為互斥型、獨立型和混合型。
1.互斥型方案的選擇
互斥方案就是相互之間存在互不相容、互相排斥關係的一組方案。互斥方案經濟效果評比的實質是判斷增量投資的經濟合理性,評比的基本方法是增量分析法,根據反映增量經濟效果的指標的不同,增量分析法可細分為靜態的差額投資收益率法和差額投資回收期法、動態的差額凈現值法和差額內部收益率法等。由於資金時間價值是客觀存在、不容忽視的,動態評價方法對互斥方案的評價更為客觀科學,因此,實際工作中,主要應用差額凈現值法和差額內部收益率法評比互斥方案,其中由差額凈現值法導出了凈現值最大準則和凈年值最大準則,凈現值最大準則用於壽命期相同的互斥方案評比,凈年值最大準則用於壽命期不同的互斥方案評比。用NPV和NAV評比互斥方案可以把絕對經濟效果評價與相對經濟效果比較結合起來,直接進行方案的選擇,而△NPV和△IRR只適用於方案的比較而不適用於方案的選擇。
2.獨立型方案的選擇
獨立方案是相互之間互不影響的一組方案。受資源限制的獨立方案的選擇方法有兩種,即獨立方案的互斥化法和雙向均衡排序法。
(1)獨立方案的互斥化法。該方法首先把各獨立方案形成互斥的方案組合;其次選出能滿足資金限制的方案組合;最後用互斥方案評選方法評選最優方案組。
該方法的優點是保證能選出受資源限制的情況下收益最大的方案組合。其不足是當獨立方案數目較多時,形成的互斥方案組的數目眾多,計算複雜:每一個獨立方案都有拒絕或接受兩種可能,如果有N個互相獨立的方案,所形成的互斥方案組合就有2n個。
(2)獨立方案的雙向均衡排序法。該方法首先計算各獨立項目的約束資源的效率,並由大到小排序,若約束資源是資金,其效率指標為NPVR或IRR;其次依次計算各方案的資源代價率及各方案組的資源總代價,各方案的資源代價率即各方案的資源消耗量,各方案組資源總代價即各方案組的資源?肖耗總量;第三畫圖並標註有關約束條件,如資源限額、基準收益率等;最後選出最優方案組。
該方法在資源充分利用的前提下,才能保證所選取的方案組是取得最大收益的方案組,但是若所選取的方案組沒有使資源完全用盡,那麼該方案組可能不是真正的最優方案組。
3.混合型方案的選擇
混合方案即互相之間既有互相獨立、又有互相排斥關係的一組方案,也稱為層混方案,即方案之間的關係分為兩個層次,高層是互相獨立的項目,而低層則由構成每個獨立項目的互斥方案組成。受資源限制的混合方案的評選也分為互斥化法和雙向均衡排序法。
(1)層混方案的互斥化法。該方法的評選步驟和優點與獨立方案的互斥化法相同,只是在形成互斥方案組合時,是從互相獨立的每個項目中,至多選出一個方案來形成各種互斥的組合。
該方法的不足也是當方案數目較多時,計算非常複雜。例如:共有M個互相獨立的項目,第t個項目有Nt個互斥方案,可以組成互相排斥的方案組合數是: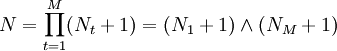 。
。
(2)層混方案的雙向均衡排序法。該方法用增量效率指標來反映互斥方案的經濟效果,所以也稱增量效率指標排序法。具體步驟:
- 淘汰無資格方案:若
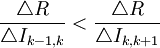 ,則方案k為無資格方案,即如果一筆基礎投資的利用效率低於其增量投資的利用效率,那麼就認為該基礎投資方案是無資格方案,應予以淘汰;
,則方案k為無資格方案,即如果一筆基礎投資的利用效率低於其增量投資的利用效率,那麼就認為該基礎投資方案是無資格方案,應予以淘汰;
- 計算有資格方案的約束資源的增量效率指標,並按該指標由大到小排序,受資金限制的層混方案的約束資源增量效率指標為△IRR、△NPVR、△R/△I等;
- 計算資源代價率及資源代價並繪圖;
- 標註資源約束條件,如資源限額、基準收益率等;
- 比選最優方案組。
該方法的不足是如果資源約束線分割了方案,那麼所選擇的方案組可能不是真正的最優方案組;如果被分割的方案恰好包含無資格方案,那麼真正的最優方案組可能恰恰包含被當作無資格方案淘汰掉的方案。
二、整數規劃在多方案選擇中的應用
傳統方法一般只能對受一種資源約束的多方案進行選擇,而整數規劃可以解決受多種資源約束的多方案選擇問題,並剋服傳統方法的不足,保證選出受資源限制情況下的收益最大的方案組合。
1.評選目標
考慮到方案間的經濟壽命可能不相等,用凈年值最大作為評選目標。
目標函數:
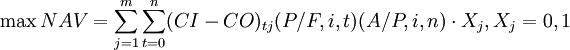 。
。
(CI − CO)tj方案j在第t年的凈現金流量;m:方案的總個數;n:方案i的經濟壽命;Xj:決策變數,Xj = 0表示放棄i方案,Xj = 1表示接受方案。
2.結束條件
由具體情況而定,一般由資源約束和關係約束組成:
(1)資源約束(資金、人工、設備、原材料等):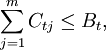 且
且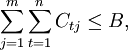 ,式中:Ctj:方案i在第t年耗用的資源量;Bt:第t年的資源可用量;B:資源總量。
,式中:Ctj:方案i在第t年耗用的資源量;Bt:第t年的資源可用量;B:資源總量。
(2)關係約束:
- 互斥方案的約束:
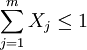 ,表示m個方案中最多只能選取一個。
,表示m個方案中最多只能選取一個。
- 獨立方案的約束:
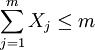 ,示m個方案中每一個都可以被選中。
,示m個方案中每一個都可以被選中。
- 混合方案的約束:
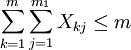 且
且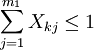 ,式中:K為互相獨立的項目數;m1為第k個項目的互斥方案數目。
,式中:K為互相獨立的項目數;m1為第k個項目的互斥方案數目。
- 從屬關係約束
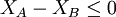 ,表示A方案只有當B方案選用時才有意義,即不選用B方案就不能選用A方案。
,表示A方案只有當B方案選用時才有意義,即不選用B方案就不能選用A方案。
- 嚴格互補關係約束:XC − XD = 0,表示C方案和方案D必須同時選用或同時不選用。
三、整數規劃對混合案選擇的例證
例如某石化公司下屬三個工廠各自獨立,分別提出互斥型投資方案,如表。各投資方案的有效期均為l0年,基準收益率為10%。如果這個公司僅有80000萬元可供投資,應如何選擇方案對公司最有利?
| 工廠 | A | B | C | ||||||
| 方案 | Al | A2 | A3 | Bl | B2 | B3 | B4 | Cl | C2 |
| 投資 | 30000 | 40000 | 50000 | l0000 | 20000 | 30000 | 40000 | 20000 | 30000 |
| 年凈收益 | 9700 | 10800 | 13800 | l630 | 5100 | 7170 | 8660 | 5000 | 8400 |
解:設目標函數為凈年值最大,則目標函數:
math>\max NAV=\sum_{j=1}^9\sum_{t=0}^10(CI-CO)_{tj}(P/F,10%,t)(A/P,10%,10)\cdot X_j,X_j=0,1</math>。
約束條件: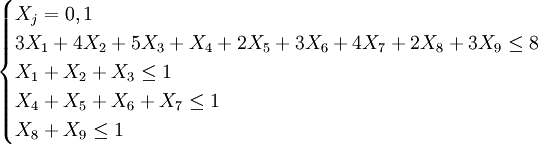 。
。
計算結果為:Xl = 1,X2 = 0,X3 = 0,X4 = 0,X5 = 1,X6 = 0,X7 = 0,X8 = 0,X9 = 1。
即應選擇Al、B2、C2三個方案。
- ↑ 王軍.整數規劃在多方案選擇中的應用[J].技術經濟,2004,(2)








建議添加整數規劃的推廣