箱线图

出自 MBA智库百科(https://wiki.mbalib.com/)

箱线图(Box plot)

　　箱线图（Boxplot）也称箱须图（Box-whisker Plot），是利用数据中的五个统计量：最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法，它也可以粗略地看出数据是否具有有对称性，分布的分散程度等信息，特别可以用于对几个样本的比较。

　　（1）画数轴

　　（2）画矩形盒 两端边的位置分别对应数据的上下四分位数矩形盒：端边的位置分别对应数据的上下四分位数（Q1和Q3）。在矩形盒内部中位数位置画一条线段为中位线。

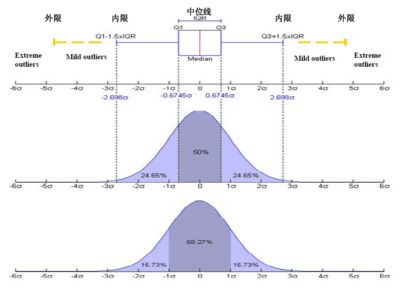
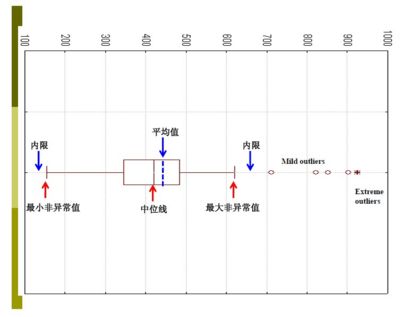
　　（3）在Q3＋1.5IQR（四分位距）和Q1-1.5IQR处画两条与中位线一样的线段，这两条线段为异常值截断点，称其为内限；在Q3＋3IQR和Q1－3IQR处画两条线段，称其为外限。处于内限以外位置的点表示的数据都是异常值，其中在内限与外限之间的异常值为温和的异常值（mild outliers），在外限以外的为极端的异常值(li)的异常值extreme outliers。

　　（4）从矩形盒两端边向外各画一条线段直到不是异常值的最远点 表示该批数据正常值的分布区间点，示该批数据正常值的分布区间。

　　（5）用“〇”标出温和的异常值，用“＊”标出极端的异常值。

　　（统计软件绘制的箱线图一般没有标出内限和外限。）

【例】^[2]12位商学院毕业生月起薪的样本在这里按升序重复如下。

　　2710 2755 2850 | 2880 2880 2890 | 2920 2940 2950 | 3050 3130 3325

　　Q₁ = 2865　Q₂ = 2905(中位数)　Q₃ = 3000

　　中位数是2 905，第一个四分位数Q₁ = 2865，第三个四分位数Q₃ = 3000。检查这些数据，最小值为2710，最大值为3325。因此，薪水数据的五数概括数据为2710、2865、2905、3000、3325。大约1／4或25％的观察值在五数概括的相邻两个数字之间。

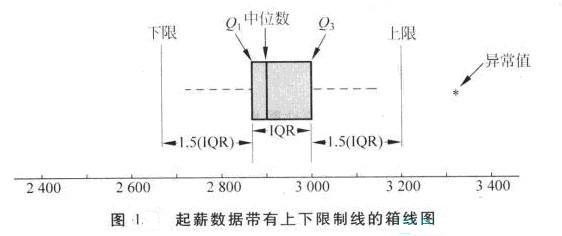
　　箱线图是在五数概括的基础上对数据进行描述的图形方法。绘制箱线图的关键是计算中位数、四分位数Q₁和Q₃。也可以使用四分位数全距IQR = Q₃ − Q₁。图1是月起薪数据的箱线图。

　　绘制箱线图的步骤如下：

　　1．画一只箱子，箱子两端分别位于第一个和第三个四分位数上。对于薪水数据来说,Q₁ = 2865以及Q₃ = 3000。这个箱子包括中间50％的数据。

　　2．在箱子中位数(薪水数据是2905)的位置画一条垂直线。

　　3．用四分位数全距IQR = Q₃ − Q₁，确定限制线的位置。箱线图的上、下限制线分别在比Q₁低1.5(IQR)和比Q₃高1.5(IQR)的位置上。对于薪水数据来说，IQR = Q₃ − Q₁ = 3000 − 2865 = 135。因此，限制线的位置在2865 − 1.5(135) = 2662.5和3000 + 1.5(135) = 3202.5处。两条限制线以外的数据可以认为是异常值。

　　4．图1中的虚线称为触须线。触须线从箱子两端开始绘制，直至第3步中计算的限制线内的最小值和最大值。因此，薪水数据的触须线分别在2 710和3 130处结束。

　　5．最后，每个异常值的位置都用星号“*”表示出来。在图1中，我们可以看到一个异常值，即3325。

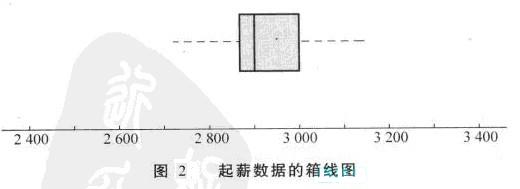
　　在图1中，我们画出了表示上下界限位置的直线。画这些线是为了说明如何计算薪水数据的限制线并标出其位置。虽然限制线通常要计算出来，但是在箱线图中一般并不标示出来。图2显示了薪水数据的常见箱线图的形状。

　　箱线图作为描述统计的工具之一，其功能有独特之处，主要有以下几点：

　　1.直观明了地识别数据批中的异常值

　　一批数据中的异常值值得关注，忽视异常值的存在是十分危险的，不加剔除地把异常值包括进数据的计算分析过程中，对结果会带来不良影响；重视异常值的出现，分析其产生的原因，常常成为发现问题进而改进决策的契机。箱线图为我们提供了识别异常值的一个标准：异常值被定义为小于Q1－1.5IQR或大于Q3＋1.5IQR的值。虽然这种标准有点任意性，但它来源于经验判断，经验表明它在处理需要特别注意的数据方面表现不错。这与识别异常值的经典方法有些不同。众所周知，基于正态分布的3σ法则或z分数方法是以假定数据服从正态分布为前提的，但实际数据往往并不严格服从正态分布。它们判断异常值的标准是以计算数据批的均值和标准差为基础的，而均值和标准差的耐抗性极小，异常值本身会对它们产生较大影响，这样产生的异常值个数不会多于总数0.7%。显然，应用这种方法于非正态分布数据中判断异常值，其有效性是有限的。箱线图的绘制依靠实际数据，不需要事先假定数据服从特定的分布形式，没有对数据作任何限制性要求，它只是真实直观地表现数据形状的本来面貌；另一方面，箱线图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响，箱线图识别异常值的结果比较客观。由此可见，箱线图在识别异常值方面有一定的优越性。

　　2.利用箱线图判断数据批的偏态和尾重

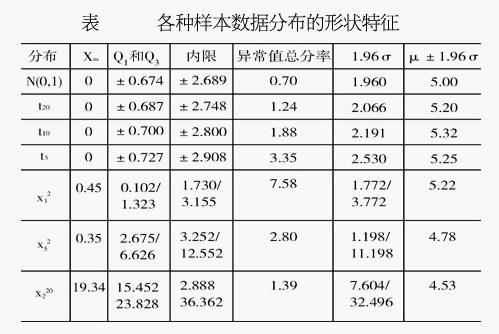
　　比较标准正态分布、不同自由度的t分布和非对称分布数据的箱线图的特征，可以发现：对于标准正态分布的大样本，只有 0.7%的值是异常值,中位数位于上下四分位数的中央,箱线图的方盒关于中位线对称。选取不同自由度的t分布的大样本，代表对称重尾分布，当t分布的自由度越小，尾部越重，就有越大的概率观察到异常值。以卡方分布作为非对称分布的例子进行分析，发现当卡方分布的自由度越小，异常值出现于一侧的概率越大，中位数也越偏离上下四分位数的中心位置，分布偏态性越强。异常值集中在较小值一侧，则分布呈现左偏态；；异常值集中在较大值一侧，则分布呈现右偏态。下表列出了几种分布的样本数据箱线图的特征（样本数据由SAS的随机数生成函数自动生成），验证了上述规律。这个规律揭示了数据批分布偏态和尾重的部分信息，尽管它们不能给出偏态和尾重程度的精确度量，但可作为我们粗略估计的依据。

　　3.利用箱线图比较几批数据的形状

　　同一数轴上，几批数据的箱线图并行排列，几批数据的中位数、尾长、异常值、分布区间等形状信息便昭然若揭。在一批数据中，哪几个数据点出类拔萃，哪些数据点表现不及一般，这些数据点放在同类其它群体中处于什么位置，可以通过比较各箱线图的异常值看出。各批数据的四分位距大小，正常值的分布是集中还是分散，观察各方盒和线段的长短便可明了。每批数据分布的偏态如何，分析中位线和异常值的位置也可估计出来。还有一些箱线图的变种，使数据批间的比较更加直观明白。例如有一种可变宽度的箱线图，使箱的宽度正比于批量的平方根，从而使批量大的数据批有面积大的箱，面积大的箱有适当的视觉效果。如果对同类群体的几批数据的箱线图进行比较，分析评价，便是常模参照解释方法的可视图示；如果把受测者数据批的箱线图与外在效标数据批的箱线图比较分析，便是效标参照解释的可视图示。箱线图结合这些分析方法用于质量管理、人事测评、探索性数据分析等统计分析活动中去，有助于分析过程的简便快捷，其作用显而易见。

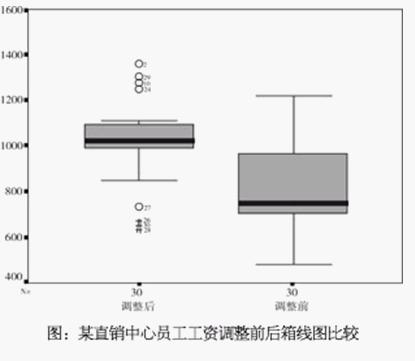
　　现有某直销中心30名员工的工资测算数据两批，第一批为工资调整前的数据，第二批为工资调整后的数据，绘出它们的箱线图（如下图），进行比较，可以很容易地得出：工资调整前，总体水平在752元左右，四分位距为307.5，没有异常值。经过调整后，箱线图显示，第2、29、10、24、27号为温和的异常值，第26、30、28号为极端的异常值。为什么会出现异常值呢？经过进一步分析知道，第2、29、10、24号员工由于技能强、工龄长、积累贡献大、表现较好，劳苦功高，理应得到较高的报酬；第27、26、30、28号职工则因为技能偏低、工龄短、积累贡献小且表现较差，得到的工资较低，甚至连一般水平也难以达到。这体现了工资调整的奖优罚劣原则。另外，调整后工资总体水平比调整前高出270元，四分位距为106，工资分布比调整前更加集中，在合适的范围内既拉开了差距，又不至于差距太悬殊，还针对特殊情况进行了特殊处理。这种工资分布具有激励作用，可以说工资调整达到预期目的。

　　箱线图美中不足之处在于它不能提供关于数据分布偏态和尾重程度的精确度量；对于批量较大的数据批，箱线图反映的形状信息更加模糊；用中位数代表总体平均水平有一定的局限性等等。所以，应用箱线图最好结合其它描述统计工具如均值、标准差、偏度、分布函数等来描述数据批的分布形状。

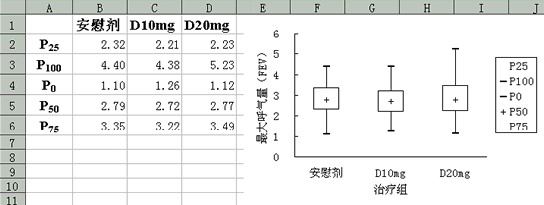
　　例：某研究者分别采用安慰剂、新药10mg、新药20mg 治疗三个随机分组的阻塞性肺病病人，每组100 例，治疗两周后测量最大呼气量（forced expiratory volume, FEV）。每组测量后计算获得的P100、P75、P50、P25、P0（即最大值、75%百分位数、中位数、25%百分位数、最小值**）（见下图），试绘制箱线图。

　　三种方案治疗阻塞性肺病后的最大呼气量箱线图

　　绘制箱线图需要借助于股价图中的“开盘-盘高-盘低-收盘图”，该图形需要将数据按一定的顺序排列。因此绘制箱线图时也需要将数据按P25、P100、P0、P50、P75的顺序排列（P25与P75的顺序可对调）。具体绘制步骤如下：

　　①选取单元格区域A1:D5，单击“图表向导”图标如果图片缩小请点击放大，在弹出的“图表类型”对话框中选中股价图的“开盘-盘高-盘低-收盘图”（第2 个子图表类型），按下一步键。

　　②在图表数据源对话框的数据区域中将“系列产生在”修改为“行”，按下一步键。

　　③在“图表选项”对话框的分类（X）轴下方填入“治疗组”，在数值（Y）轴下方填入“最大呼气量（FEV）”，按完成键。

　　④在绘图区点击右键，选取“数据源→系列→添加”，在“名称”右侧用鼠标选取单元格A6，在“值”右侧用鼠标选取单元格区域B6:D6 按确定键。

　　⑤在网格线上点击右键，“清除”网格线；在绘图区单击右键“清除”背景色。

　　⑥在横坐标上单击右键，选取“坐标轴格式→图案”，右上部主要刻度线类型复选“无”，按确定键。

　　⑦在纵坐标上单击右键，选取“坐标轴格式→数字→数值”，小数位数改为“0”，按确定键。

　　⑧在箱的中心位置P50 系列标志上单击右键，选取“数据系列格式→图案”，在界面右侧数据标记的样式处选取“+”，前景颜色处选黑色，“大小”改为6 磅，按确定键；在箱线图的顶部P100系列标志上单击右键，选取“数据系列格式→图案”，在界面右侧数据标记的样式处选取长横线“－”，前景颜色处选黑色，“大小”改为6 磅，按确定键；在箱线图的底部P0系列标志上单击右键，选取“数据系列格式→图案”，在界面右侧数据标记的样式处选取长横线“－”，前景颜色处选黑色， “大小”改为6 磅，按确定键。

　　⑨适当调整绘图区的大小，调整整个图表区域的字体大小，去除图表区的边框等，可获得上图右侧的箱线图。

• 注：这五个值可以在Excel中用QUARTILE(array,quart)函数求得。由此处也可知，用Excel作箱线图实际上也是一种间接的方式，并不是像SPSS等软件那样直接生成，从统计的角度来说，更重要的是这种方法不考虑Outliers，所以与其他软件作出来的图可能并不一样。

　　1、不能提供关于数据分布偏态和尾重程度的精确度量

　　2、对于批量比较大的数据批，反应的形状信息更加模糊

　　3、用中位数代表总体评价水平有一定的局限性