估计量
出自 MBA智库百科(https://wiki.mbalib.com/)
估计量(estimator)
目录 |
估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
估计量的优良性准则[1]
1.无偏性
估计量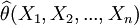 是一个随机变量,对一次具体的观察或试验的结果,估计值可能较真实的参数值有一定偏离,但一个好的估计量不应总是偏小或偏大,在多次试验中所得估计量的平均值应与参数的真值相吻合,这正是无偏性的要求。
是一个随机变量,对一次具体的观察或试验的结果,估计值可能较真实的参数值有一定偏离,但一个好的估计量不应总是偏小或偏大,在多次试验中所得估计量的平均值应与参数的真值相吻合,这正是无偏性的要求。
【定义1】 设(X1,X2,...,Xn)为来自总体X的样本,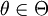 为总体的未知参数,
为总体的未知参数,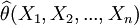 为θ的一个估计量.若对于任意
为θ的一个估计量.若对于任意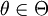 有
有
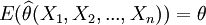 (1)
(1)
则称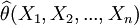 为θ的无偏估计量.记
为θ的无偏估计量.记
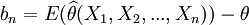
称bn以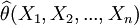 作为θ的估计的偏差,当
作为θ的估计的偏差,当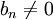 时,称
时,称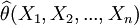 为θ的有偏估计量,若
为θ的有偏估计量,若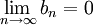 则称
则称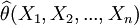 是θ的渐近无偏估计.
是θ的渐近无偏估计.
无偏性的意义是,用一个估计量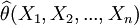 去估计未知参数θ,有时候可能偏高,有时候可能偏低,但是平均来说它等于未知参数θ。
去估计未知参数θ,有时候可能偏高,有时候可能偏低,但是平均来说它等于未知参数θ。
【定理1】 设对总体X,有E(X) = μ,D(X) = σ2从总体X中抽取样本X1,X2,...,Xn用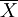 ,S2分别表示样本均值和样本修正方差,则
,S2分别表示样本均值和样本修正方差,则
(1)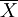 是 μ 的无偏估计量;
是 μ 的无偏估计量;
(2)S2是 σ2的无偏估计量.
证 由题设,E(Xi) = μ,D(Xi) = σ2(i = 1,2,...,n),且诸Xi独立。于是有
(1)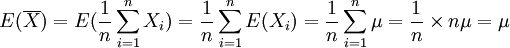 ,即
,即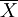 是总体均值μ的无偏估计量。
是总体均值μ的无偏估计量。
(2)因总体X的期望E(X) = μ和方差D(X) = σ2存在,则
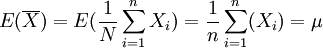
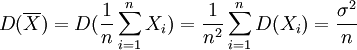
![E(S^2)=\frac{1}{n-1} E[\sum^n_{i=1} (X_i - \overline{X})^2]](/w/images/math/d/7/8/d7870773872a53bb6c53fc58b20e0b17.png)
![=\frac{1}{n-1} E [\sum^n_{i=1} X^2_i - n \overline{X}^2]](/w/images/math/b/8/d/b8dd3b0b250ce8b82a7cab8c3070c0d9.png)
![=\frac{1}{n-1} [\sum^n_{i=1} E(X^2_i) - nE (\overline{X}^2)]](/w/images/math/8/c/c/8cca806f63cb7446ba50f56cd1741aba.png)
![=\frac{1}{n-1} \sum^n_{i=1} \left\{D(X_i) + [E(X_i)]^2 \right\} - \frac{n}{n-1} \left\{D(\overline{X}) + [E(\overline{X})]^2 \right\}](/w/images/math/b/4/3/b4364b75d80eedf7bb8ce173f733b2b0.png)
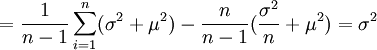
故S2是总体方差σ2的无偏估计量.
但对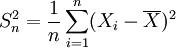 ,有
,有
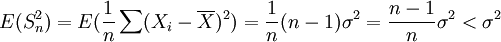
若n很大时,则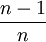 很接近1,表明
很接近1,表明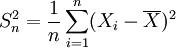 不是 σ2 的无偏估计,而是σ2的渐近无偏估计。
不是 σ2 的无偏估计,而是σ2的渐近无偏估计。
【例1】 设总体X的k阶矩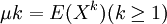 存在,(X1,X2,...,Xn)为来
存在,(X1,X2,...,Xn)为来
自总体X的样本,试证明不论总体X服从什么分布,k阶样本矩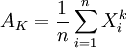 是k阶总体矩μk的无偏估计.
是k阶总体矩μk的无偏估计.
证 X1,X2,...,Xn与X同分布,故有
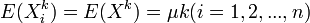
即有
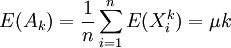
【例2】 设总体X服从参数为λ的指数分布,其概率密度为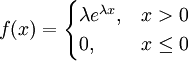
其中参数λ > 0 但未知,又设X1,X2,...,Xn为来自总体X的样本,试证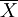 和nZ = n[min(X1,X2,...,Xn)]都是1 / λ的无偏估计.
和nZ = n[min(X1,X2,...,Xn)]都是1 / λ的无偏估计.
证 因E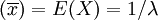 ,所以
,所以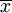 是1 / λ的无偏估计量.而Z = [min(X1,X2,...,Xn)]具有概率密度
是1 / λ的无偏估计量.而Z = [min(X1,X2,...,Xn)]具有概率密度
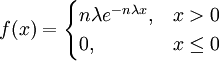
故知E(Z) = 1 / nλ,从而E(nZ) = 1 / λ,即nZ也是1 / λ的无偏估计量
此例结果表明,一个未知参数可以有不同的无偏估计量.值得注意,若 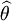 是 θ的无偏估计,g(θ)是θ的函数,
是 θ的无偏估计,g(θ)是θ的函数,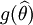 不一定是g(θ)的无偏估计.
不一定是g(θ)的无偏估计.
【例3】 试证样本标准差S不是总体标准差 σ 的无偏估计.
证 因为σ2 = E(S2) = D(S) + [E(S)]2,注意到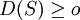 ,所以
,所以![\sigma^2 \ge [E(S)]^2](/w/images/math/0/0/1/00137301e2bd0355826750f6e7397bf3.png) ,于是
,于是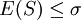 ,这表明尽管S2是σ2的无偏估计,但S不是总体标准差σ的无偏估计.用样本标准差S去估计总体的标准差 σ ,平均来说是偏低了.
,这表明尽管S2是σ2的无偏估计,但S不是总体标准差σ的无偏估计.用样本标准差S去估计总体的标准差 σ ,平均来说是偏低了.
2.有效性
用样本统计量作为总体参数的估计量,其无偏性是重要的,但同一参数的无偏估计不是唯一的,还应该从中选取最好的.例如,从总体X中抽取样本X1,X2,X3,则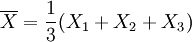 是总体均值 μ 的无偏估计.考虑E(Xi) = μ,则每个Xi也都是 μ 的无偏估计.还有
是总体均值 μ 的无偏估计.考虑E(Xi) = μ,则每个Xi也都是 μ 的无偏估计.还有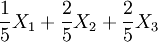 , 其数学期望也是μ,它也是μ的无偏估计。
, 其数学期望也是μ,它也是μ的无偏估计。
一般只要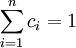 ,
, 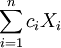 就是μ的无偏估计.这么多无偏估计中哪一个更好一些呢?这就有了有效性的概念.
就是μ的无偏估计.这么多无偏估计中哪一个更好一些呢?这就有了有效性的概念.
对于参数 θ 的无偏估计量,其取值应在真值附近波动,我们自然希望它与真值之间的偏差越小越好,也就是说无偏估计量的方差越小越好.
【定义2】 设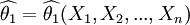 与
与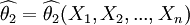 均为未知参数θ的无偏估计量,若
均为未知参数θ的无偏估计量,若
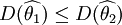 (2)
(2)
则称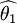 比
比 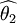 有效
有效
【定理2】 总体均值μ的所有线性无偏估计中,以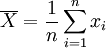 最为有效。
最为有效。
证 μ的所有线性无偏估计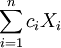 ,中
,中 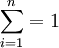 其方差
其方差
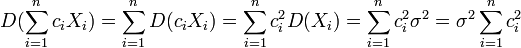
要求这个方差的最小值,相当于求函数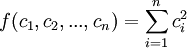 ,在条件
,在条件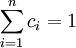 下的最小值.这是一个条件极值问题,用拉格朗日乘数法,令
下的最小值.这是一个条件极值问题,用拉格朗日乘数法,令

由 
得 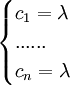
即c1 = c2 = ... = cn
代入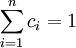 ,则
,则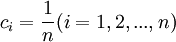 。
。
这是唯一驻点,应是极小值点,亦是最小值点,即当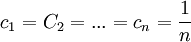 时,
时,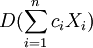 达到最小,即
达到最小,即
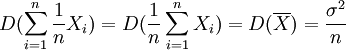
为方差最小值.这表明在总体均值μ的所有线性无偏估计中,以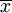 最为有效.
最为有效.
【例4】(续例2)在例2的条件下,试证当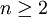 时,θ的无偏估计量
时,θ的无偏估计量 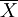 比无偏估计量nZ有效.
比无偏估计量nZ有效.
证 因为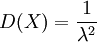 ,所以
,所以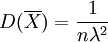 .再由Z的密度函数可得
.再由Z的密度函数可得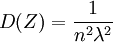 ,故有
,故有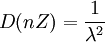 。当
。当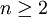 时
时 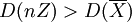 ,故
,故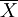 比nZ有效.
比nZ有效.
在θ的所有无偏估计量中,若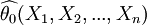 是具有最小方差的无偏估计量,则称
是具有最小方差的无偏估计量,则称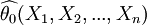 为θ的一致最小方差无偏估计量最优无偏估计量.
为θ的一致最小方差无偏估计量最优无偏估计量.
可以证明,无偏估计量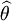 的方差
的方差 的下界D0(θ)为
的下界D0(θ)为
![D(\widehat{\theta}) \ge D_0 (\theta) = \frac{1}{nE[\frac{\partial}{\partial \theta} lnf (X, \theta)]^2} > 0](/w/images/math/3/6/f/36fe2c065800df9fa03d00f94f123b50.png)
当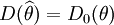 时,
时,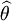 就是θ的最优无偏估计量.这里,f(x,θ)表示连续型随机变量的概率密度或离散型随机变量的概率函数.
就是θ的最优无偏估计量.这里,f(x,θ)表示连续型随机变量的概率密度或离散型随机变量的概率函数.
【例5】 设总体X服从参数为λ的泊松分布,X1,X2,...,Xn是来自该总体的一个样本,求参数λ的极大似然估计量 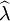 ,并证明
,并证明 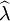 是参数λ的最优估计量.
是参数λ的最优估计量.
解 设样本的一个观察值为X1,X2,...,Xn,则似然函数
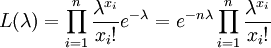
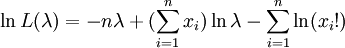
令
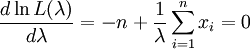
得 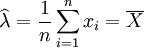
由于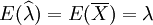 ,故
,故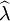 是参数λ的无偏估计量.
是参数λ的无偏估计量.
又因
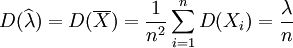
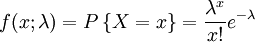
lnf(x;λ) = − λ + xlnλ − ln(x!)
![E \left\{[\frac{\partial}{\partial \lambda} \ln f(X; \lambda)]^2 \right\} = E[ \frac{1}{\lambda^2}(X - \lambda)^2] = \frac{1}{\lambda^2} E[X-E(X)]^2 = \frac{1}{\lambda^2} D(X) =\frac{1}{\lambda}](/w/images/math/8/0/4/8044f3743a6ea3a4c91e5647cdef30ca.png)
所以
![D_0(\widehat{\lambda}) = \frac{1}{nE \left\{ [\frac{\partial}{\partial \lambda} \ln f(X; \lambda)]^2 \right\}} = \frac{\lambda}{n}](/w/images/math/3/2/1/321736e4d9e6b5e799c89238553ef194.png)
因此,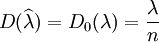 ,即
,即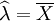 是参数λ的最优估计量
是参数λ的最优估计量
3.一致性
上面从无偏性和有效性两个方面讨论了选择估计量的标准,但它们都是在固定样本容量竹的前提下提出的.容易想象,如果样本容量越大,样本所含的总体分布的信息应该越多,我们希望随着样本容量的增大,估计量的值能够稳定于待估参数的真值,估计量的这种性质称为一致性.
【定义3】设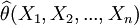 为参数θ的估计量,若对于任意
为参数θ的估计量,若对于任意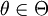 及任意ε > O,有
及任意ε > O,有
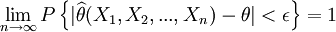 (3)
(3)
即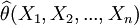 依概率收敛于θ,则称
依概率收敛于θ,则称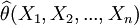 为θ的一致估计量(或相合估计量).
为θ的一致估计量(或相合估计量).
【例6】证明样本k阶原点矩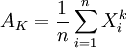 是总体k阶原点矩
是总体k阶原点矩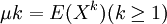 的一致估计.
的一致估计.
证由于X1,X2,...,Xn相互独立与X同分布,所以对任意 ,
, 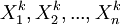 也相互独立与Xk同分布.因此,由大数定律,对于任意ε > 0,有
也相互独立与Xk同分布.因此,由大数定律,对于任意ε > 0,有
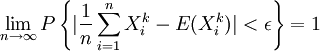
此表明Ak是 μk的一致估计量.
进而,若待估参数θ = g(μ1,μ2,...,μk),其中g(·)为连续函数,则θ的估计量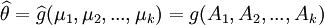 (这里Ak为样本k阶原点矩)是θ的一致估计量。由此可证,样本方差 S2 是总体方差σ2 的一致估计量。
(这里Ak为样本k阶原点矩)是θ的一致估计量。由此可证,样本方差 S2 是总体方差σ2 的一致估计量。
- ↑ 陈荣江,王建平主编.概率论与数理统计.科学出版社,2012.03







