峰度
出自 MBA智库百科(https://wiki.mbalib.com/)
峰度(Peakness/Kurtosis)又稱峰態繫數
目錄 |
峰度是指次數分佈曲線頂峰的尖平程度,是次數分佈的又一重要特征。統計上,常以正態分佈曲線為標準,來觀察比較某一次數分佈曲線的頂端正黨風尖頂或平頂以及尖平程度的大小。
根據變數值的集中與分散程度,峰度一般可表現為三種形態:尖頂峰度、平頂峰度和標準峰度。當變數值的次數在眾數周圍分佈比較集中,使次數分佈曲線比正態分佈曲線頂峰更為隆起尖峭,稱為尖頂峰度;當變數值的次數在眾數周圍分佈較為分散,使次數分佈曲線較正態分佈曲線更為平緩,稱為平頂峰度。可見,尖頂峰度或平頂峰度都是相對正態分佈曲線的標準峰度而言的。
峰度的測定,一般是採用統計動差方法,即以四階中心動差V4為測定依據,將V4除以其標準差的四次方σ4,以消除單位量綱的影響,便於不同次數分佈曲線的峰度比較,從而得到以無名數表示的相對數,即為峰度的測定值(β)。計算公式為:
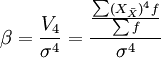
由統計計算分析可知,當次數分佈為正態分佈曲線時,β = 3,以此為標準就可比較分析各種次數分佈曲線的峰度。當β > 3時,表示分佈曲線呈尖頂峰度,為尖頂曲線,說明變數值的次數較為密集地分佈在眾數的周圍,β值越大於3,分佈曲線的頂端越尖峭。當β < 3時,表示分佈曲線呈平頂峰度,為平頂曲線,說明變數值的次數分佈比較均勻地分散在眾數的兩側,β值越小於3,則分佈曲線的頂峰就越平緩。一般當β值接近於1.8時,分佈曲線呈水平矩形分佈形態,說明各組變數值的次數相同。當β值小於1.8時,次數分佈曲線趨向“U”型分佈。實際統計分析中,通常將偏度和峰度結合起來運用,以判斷變數分佈是否接近於正態分佈。







