峰度

出自 MBA智库百科(https://wiki.mbalib.com/)

峰度(Peakness/Kurtosis)又称峰态系数

　　峰度是指次数分布曲线顶峰的尖平程度，是次数分布的又一重要特征。统计上，常以正态分布曲线为标准，来观察比较某一次数分布曲线的顶端正党风尖顶或平顶以及尖平程度的大小。

　　根据变量值的集中与分散程度，峰度一般可表现为三种形态：尖顶峰度、平顶峰度和标准峰度。当变量值的次数在众数周围分布比较集中，使次数分布曲线比正态分布曲线顶峰更为隆起尖峭，称为尖顶峰度；当变量值的次数在众数周围分布较为分散，使次数分布曲线较正态分布曲线更为平缓，称为平顶峰度。可见，尖顶峰度或平顶峰度都是相对正态分布曲线的标准峰度而言的。

　　峰度的测定，一般是采用统计动差方法，即以四阶中心动差V₄为测定依据，将V4除以其标准差的四次方σ⁴，以消除单位量纲的影响，便于不同次数分布曲线的峰度比较，从而得到以无名数表示的相对数，即为峰度的测定值（β）。计算公式为：

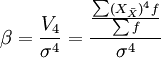
　　　　由统计计算分析可知，当次数分布为正态分布曲线时，β = 3，以此为标准就可比较分析各种次数分布曲线的峰度。当β > 3时，表示分布曲线呈尖顶峰度，为尖顶曲线，说明变量值的次数较为密集地分布在众数的周围，β值越大于3，分布曲线的顶端越尖峭。当β < 3时，表示分布曲线呈平顶峰度，为平顶曲线，说明变量值的次数分布比较均匀地分散在众数的两侧，β值越小于3，则分布曲线的顶峰就越平缓。一般当β值接近于1.8时，分布曲线呈水平矩形分布形态，说明各组变量值的次数相同。当β值小于1.8时，次数分布曲线趋向“U”型分布。实际统计分析中，通常将偏度和峰度结合起来运用，以判断变量分布是否接近于正态分布。