遺傳演算法
出自 MBA智库百科(https://wiki.mbalib.com/)
遺傳演算法(Genetic Algorithm)
目錄 |
遺傳演算法是一類借鑒生物界的進化規律(適者生存,優勝劣汰遺傳機制)演化而來的隨機化搜索方法。它是由美國的J.Holland教授1975年首先提出,其主要特點是直接對結構對象進行操作,不存在求導和函數連續性的限定;具有內在的隱並行性和更好的全局尋優能力;採用概率化的尋優方法,能自動獲取和指導優化的搜索空間,自適應地調整搜索方向,不需要確定的規則。遺傳演算法的這些性質,已被人們廣泛地應用於組合優化、機器學習、信號處理、自適應控制和人工生命等領域。它是現代有關智能計算中的關鍵技術之一。
達爾文的自然選擇學說是一種被人們廣泛接受的生物進化學說。這種學說認為,生物要生存下去,就必須進行生存鬥爭。生存鬥爭包括種內鬥爭、種間鬥爭以及生物跟無機環境之間的鬥爭三個方面。在生存鬥爭中,具有有利變異的個體容易存活下來,並且有更多的機會將有利變異傳給後代;具有不利變異的個體就容易被淘汰,產生後代的機會也少的多。因此,凡是在生存鬥爭中獲勝的個體都是對環境適應性比較強的。達爾文把這種在生存鬥爭中適者生存,不適者淘汰的過程叫做自然選擇。它表明,遺傳和變異是決定生物進化的內在因素。自然界中的多種生物之所以能夠適應環境而得以生存進化,是和遺傳和變異生命現象分不開的。正是生物的這種遺傳特性,使生物界的物種能夠保持相對的穩定;而生物的變異特性,使生物個體產生新的性狀,以致於形成新的物種,推動了生物的進化和發展。
遺傳演算法是模擬達爾文的遺傳選擇和自然淘汰的生物進化過程的計算模型。它的思想源於生物遺傳學和適者生存的自然規律,是具有“生存+檢測”的迭代過程的搜索演算法。遺傳演算法以一種群體中的所有個體為對象,並利用隨機化技術指導對一個被編碼的參數空間進行高效搜索。其中,選擇、交叉和變異構成了遺傳演算法的遺傳操作;參數編碼、初始群體的設定、適應度函數的設計、遺傳操作設計、控制參數設定五個要素組成了遺傳演算法的核心內容。 作為一種新的全局優化搜索演算法,遺傳演算法以其簡單通用、魯棒性強、適於並行處理以及高效、實用等顯著特點,在各個領域得到了廣泛應用,取得了良好效果,並逐漸成為重要的智能演算法之一。
長度為L的n個二進位串bi(i=1,2,…,n)組成了遺傳演算法的初解群,也稱為初始群體。在每個串中,每個二進位位就是個體染色體的基因。根據進化術語,對群體執行的操作有三種:
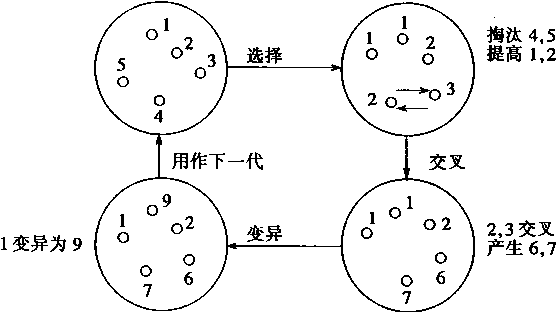
1.選擇(Selection)
這是從群體中選擇出較適應環境的個體。這些選中的個體用於繁殖下一代。故有時也稱這一操作為再生(Reproduction)。由於在選擇用於繁殖下一代的個體時,是根據個體對環境的適應度而決定其繁殖量的,故而有時也稱為非均勻再生(differential reproduction)。
2.交叉(Crossover)
這是在選中用於繁殖下一代的個體中,對兩個不同的個體的相同位置的基因進行交換,從而產生新的個體。
3.變異(Mutation)
這是在選中的個體中,對個體中的某些基因執行異向轉化。在串bi中,如果某位基因為1,產生變異時就是把它變成0;反亦反之。
遺傳演算法的原理可以簡要給出如下:
choose an intial population
determine the fitness of each individual
perform selection
repeat
perform crossover
perform mutation
determine the fitness of each individual
perform selection
until some stopping criterion applies
這裡所指的某種結束準則一般是指個體的適應度達到給定的閥值;或者個體的適應度的變化率為零。
1.初始化
選擇一個群體,即選擇一個串或個體的集合bi,i=1,2,...n。這個初始的群體也就是問題假設解的集合。一般取n=30-160。通常以隨機方法產生串或個體的集合bi,i=1,2,...n。問題的最優解將通過這些初始假設解進化而求出。
2.選擇
根據適者生存原則選擇下一代的個體。在選擇時,以適應度為選擇原則。適應度準則體現了適者生存,不適應者淘汰的自然法則。
給出目標函數f,則f(bi)稱為個體bi的適應度。以
為選中bi為下一代個體的次數。
顯然.從式(3—86)可知:
(1)適應度較高的個體,繁殖下一代的數目較多。
(2)適應度較小的個體,繁殖下一代的數目較少;甚至被淘汰。
這樣,就產生了對環境適應能力較強的後代。對於問題求解角度來講,就是選擇出和最優解較接近的中間解。
3.交叉
對於選中用於繁殖下一代的個體,隨機地選擇兩個個體的相同位置,按交叉概率P。在選中的位置實行交換。這個過程反映了隨機信息交換;目的在於產生新的基因組合,也即產生新的個體。交叉時,可實行單點交叉或多點交叉。
例如有個體
S1=100101
S2=010111
選擇它們的左邊3位進行交叉操作,則有
S1=010101
S2=100111
一般而言,交叉幌宰P。取值為0.25—0.75。
4.變異
根據生物遺傳中基因變異的原理,以變異概率Pm對某些個體的某些位執行變異。在變異時,對執行變異的串的對應位求反,即把1變為0,把0變為1。變異概率Pm與生物變異極小的情況一致,所以,Pm的取值較小,一般取0.01-0.2。
例如有個體S=101011。
對其的第1,4位置的基因進行變異,則有
S'=001111
單靠變異不能在求解中得到好處。但是,它能保證演算法過程不會產生無法進化的單一群體。因為在所有的個體一樣時,交叉是無法產生新的個體的,這時只能靠變異產生新的個體。也就是說,變異增加了全局優化的特質。
5.全局最優收斂(Convergence to the global optimum)
當最優個體的適應度達到給定的閥值,或者最優個體的適應度和群體適應度不再上升時,則演算法的迭代過程收斂、演算法結束。否則,用經過選擇、交叉、變異所得到的新一代群體取代上一代群體,並返回到第2步即選擇操作處繼續迴圈執行。
圖3—7中表示了遺傳演算法的執行過程
1.遺傳演算法從問題解的中集開始嫂索,而不是從單個解開始。
這是遺傳演算法與傳統優化演算法的極大區別。傳統優化演算法是從單個初始值迭代求最優解的;容易誤入局部最優解。遺傳演算法從串集開始搜索,覆蓋面大,利於全局擇優。
2.遺傳演算法求解時使用特定問題的信息極少,容易形成通用演算法程式。
由於遺傳演算法使用適應值這一信息進行搜索,並不需要問題導數等與問題直接相關的信息。遺傳演算法只需適應值和串編碼等通用信息,故幾乎可處理任何問題。
3.遺傳演算法有極強的容錯能力
遺傳演算法的初始串集本身就帶有大量與最優解甚遠的信息;通過選擇、交叉、變異操作能迅速排除與最優解相差極大的串;這是一個強烈的濾波過程;並且是一個並行濾波機制。故而,遺傳演算法有很高的容錯能力。
4.遺傳演算法中的選擇、交叉和變異都是隨機操作,而不是確定的精確規則。
這說明遺傳演算法是採用隨機方法進行最優解搜索,選擇體現了向最優解迫近,交叉體現了最優解的產生,變異體現了全局最優解的覆蓋。
5.遺傳演算法具有隱含的並行性
遺傳演算法在神經網路中的應用主要反映在3個方面:網路的學習,網路的結構設計,網路的分析。
1.遺傳演算法在網路學習中的應用
在神經網路中,遺傳演算法可用於網路的學習。這時,它在兩個方面起作用
(1)學習規則的優化
用遺傳演算法對神經網路學習規則實現自動優化,從而提高學習速率。
(2)網路權繫數的優化
用遺傳演算法的全局優化及隱含並行性的特點提高權繫數優化速度。
2.遺傳演算法在網路設計中的應用
用遺傳演算法設計一個優秀的神經網路結構,首先是要解決網路結構的編碼問題;然後才能以選擇、交叉、變異操作得出最優結構。編碼方法主要有下列3種:
(1)直接編碼法
這是把神經網路結構直接用二進位串表示,在遺傳演算法中,“染色體”實質上和神經網路是一種映射關係。通過對“染色體”的優化就實現了對網路的優化。
(2)參數化編碼法
參數化編碼採用的編碼較為抽象,編碼包括網路層數、每層神經元數、各層互連方式等信息。一般對進化後的優化“染色體”進行分析,然後產生網路的結構。
(3)繁衍生長法
這種方法不是在“染色體”中直接編碼神經網路的結構,而是把一些簡單的生長語法規則編碼入“染色體”中;然後,由遺傳演算法對這些生長語法規則不斷進行改變,最後生成適合所解的問題的神經網路。這種方法與自然界生物地生長進化相一致。
3.遺傳演算法在網路分析中的應用
遺傳演算法可用於分析神經網路。神經網路由於有分佈存儲等特點,一般難以從其拓撲結構直接理解其功能。遺傳演算法可對神經網路進行功能分析,性質分析,狀態分析。
遺傳演算法雖然可以在多種領域都有實際應用,並且也展示了它潛力和寬廣前景;但是,遺傳演算法還有大量的問題需要研究,目前也還有各種不足。首先,在變數多,取值範圍大或無給定範圍時,收斂速度下降;其次,可找到最優解附近,但無法精確確定最擾解位置;最後,遺傳演算法的參數選擇尚未有定量方法。對遺傳演算法,還需要進一步研究其數學基礎理論;還需要在理論上證明它與其它優化技術的優劣及原因;還需研究硬體化的遺傳演算法;以及遺傳演算法的通用編程和形式等。
案例一:遺傳演算法在裝箱環節中的應用[1]
一、一維裝箱問題的描述
一維裝箱問題[2]引可描述如下:
要將11個物品裝入許多箱子(最多n個箱子)。每個物品有重量(Wj > 0)。每個箱子有重量限制(ci > O)。問題是尋找最好的將物品分配到箱子的方案,使得在每個箱子中物品的總重量不超過其限制,並且使用的箱子數量最少。
該問題可表示[2]為:
重量及限製表
| 物品 | 1 | 2 | \ldots | n |
| 重量 | w_1 | w_2 | \ldots | w_n |
| 重量限制 | c_1 | c_2 | \ldots | c_n |
其中重量Wj和重量限制ci是正實數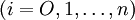 裝箱問題的數學表示如下:
裝箱問題的數學表示如下:
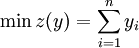 。
。
 i\in N=\left\{1,2,\ldots,n\right\}。
i\in N=\left\{1,2,\ldots,n\right\}。
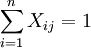
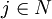 。
。
yi=0或1 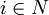 xij=0或1
xij=0或1 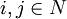 。
。
其中yi = l表示箱子i被放入物品,反之則表示箱子i空著;Xij = 1表示物品j放入箱子i,反之表示物品j未放入箱子i。
基於基本遺傳演算法的求解方案。
由於近似演算法有時並不能產生出一個優秀的裝箱方案,在這裡採用遺傳演算法進行優化。
(一)染色體表示
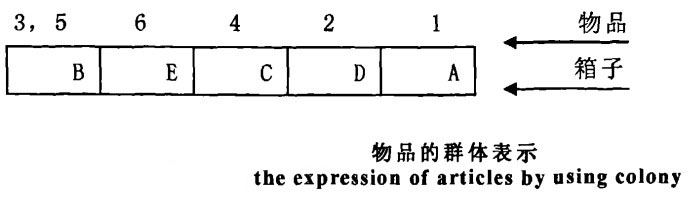
對於一維裝箱問題,由於其裝箱費用依賴於箱子中物體的群體,故在此問題中染色體的表示需要包含兩個部分,其一應該提供哪個物品屬於哪個箱子(群體)的信息,另外對使用的箱子進行編碼。故採用基於群體的表示方法[2],其中一個基因表示一個箱子。
設有六個物品,從1到6對其進行編碼,染色體物品部分可以寫作1 4 2 3 2 5。表示第一個物品放入箱子1,第二個物品放入箱子4,第三個和第五個物品放入箱子2,第四個物品放入箱子3,第六個物品放入箱子5。染色體的群體部分僅表示箱子。下麵我們採用字母而不是整數來表示箱子(比如,上述染色體可表示為ADBCBE)。通過查詢物品部分,可知群體的名字代表的含義,即A={1),B=(3,5),c={4),D=(2),E=(6)。
包含兩部分的染色體的集成用圖表示如下:
(二)初始化種群
由於BFD演算法對於很多數據均有較好的效果,所以本程式中把BFD演算法作為一種方案放入初始的群體,這樣就可能不失去一些優秀的解。
(三)選擇運算元
選擇操作是建立在群體中個體的適應度的評估的基礎上,在本演算法中採用按正比與適應度的輪盤賭的方式進行隨機選擇,為了提高效率,選擇輪盤時採用折半查找的方法,這樣就能有效地減少比較次數,確保該過程的時間複雜度為0(log n)(n為種群大小)。
(四)雜交運算元
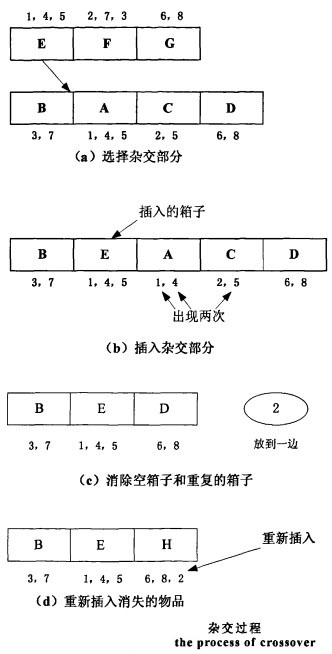
因為染色體的表示包含兩個部分:箱子和物品的群體。因此需要處理可變長度的染色體,故其雜交過程[2]如下:
第一步:隨機選擇兩個雜交位置,對每個父代選定雜交部分
第二步:將第一個父代雜交部分的內容插入到第二個父代第一個雜交位置之前。由於雜交對染色體的部分群體進行操作,這就意味著從第一個父代插入一些群體(箱子)到第二個父代中。
第三步:從產生的後代中原有的箱子中去掉所有重覆出現的物品,使得這些物品原先的從屬關係讓位於“新”插入的箱子。因此產生的後代中的某些群體發生了改變。他們不再包含與先前相同的物品,原因是消除了一些物品。
第四步:改變兩個父代的角色並重新應用第二步到第三步生成第2個子代。
雜交過程可用圖表示:
(五)變異運算元
裝箱問題的變異運算元必須針對箱子進行操作,一般有兩種策略:啟用一個新箱子或消除一個已經使用的箱子。
(六)適應度函數
裝箱問題的目標是:最小化使用的箱子數量同時儘量裝滿所使用的箱子。根據此要求,本文采用玄光南等所編教材《遺傳演算法與工程優化》中提到的適應度函數[2]。具體定義如下:
 。
。
其中,N是解中使用的箱子數量,Fi是第i個箱子中所裝有物品的重量之和,C是箱子的重量限制,k是常數(k>1)。常數k表示了對裝得滿的箱子的重視程度。k越大,裝得滿的箱子比一般填充的箱子受到的重視就越大。一般,k取值為2得到的結果較好。
二、求解步驟
(一)確定問題的解空間和個體的表現型
我們把染色體表示為含有物品和箱子兩項信息的數據串。首先對待裝物品進行編號1-n,對箱子進行編號1-k,按照物品編號順序寫出其所在箱子的編號序列即定義為染色體。具體含義在上節中介紹的比較詳細,這裡將不再贅述。
(二)建立優化模型,確定出目標函數
該問題錶面上是要求得所用箱子的最小數目,其實是最大化利用資源的問題,故目標函數的類型應該是求最大值的。由此,我們採用的適應度函數為。
 其中,N是解中使用的箱子數量,Fi是第i個箱子中所裝有物品的重量之和,C是箱子的重量限制,k取值為2。
其中,N是解中使用的箱子數量,Fi是第i個箱子中所裝有物品的重量之和,C是箱子的重量限制,k取值為2。
(三)確定遺傳運算元
見上節中對選擇、交叉、變異三種遺傳運算元的設定,這裡不再贅述。
(四)確定運行參數
本文中,我們設定交叉概率Pc = 0.7,變異概率Pn = 0.1,代數gen=100,種群大小n=100。
三、計算舉例與結果分析。
為了闡明利用該演算法的計算過程與結果,程式選定下列一組特殊數據:假設現有一個由l5個物體組成的物體隊列和足夠多的單位箱子,其中物體的重量如下:1-9號物品的重量:0.310-l5號物品的重量:0.2假設箱子容量為1,按照BFD演算法,我們可以得到下列裝箱方案:。
(O.3,O.3,O.3),(0.3,0.3,0.3),(0.3,O.3,O.3),(O.2,0.2,0.2,0.2,0.2),(0.2)共用了5個箱子。
我們把上述利用BFD演算法產生的裝箱方案作為利用遺傳演算法進行求解的初始群體,同時,我們取交叉概率Pc = 0.7,變異概率Pn = 0.1,代數gen=100,種群大小n--100。得出結果為:(0.3,0.3,0.2,0.2),(0.3,0.3,0.2,0.2),(0.3,0.3,0.2,0.2),(0.3,0.3,0.3)共四個箱子,顯然結果比較理想。
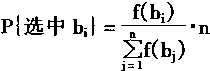








不是大學生看不懂