37%法則
出自 MBA智库百科(https://wiki.mbalib.com/)
37%法則、37%規則
目錄 |
37%法則,出自《演算法之美》[1]一書。意思是經過數學家歐拉的實驗,以37%作為分界點,前面的時間用來觀察,後面的時間用來作決策的一種方法。
舉例來說,比如要買房子,整個地區的房子有30處,那麼需要先看37%的房子,也就是11個房子。37%前的房子只看不買,但是要記住自己認為最好的是什麼樣子。看完後,從37%以後只有遇到比之前最好的還要好的房子就應該下手買。
有這麼一個故事:一天,蘇格拉底帶領幾個弟子來到一塊麥地邊。他對弟子們說:“你們去麥地里摘一個最大的麥穗,只許前行不能回頭,我在麥地的盡頭等你們。”弟子們低頭前行,挑挑揀揀,總覺得最大的麥穗還在前面。雖然,有弟子試著摘了幾穗,但並不滿意,便隨手扔掉了。他們總以為機會還很多,完全沒有必要過早定奪。過了很久,很多弟子還是兩手空空。這時,傳來蘇格拉底的聲音:“你們已經到盡頭了。”是如弟子們一樣二手空空,還是如蘇格拉底所說,“麥地里肯定有一穗是最大的,但你們未必能碰到它;即便碰到,也未必能作出準確的判斷。因此最大的一穗就是你們剛剛摘下的。”
相似的問題,有一片玉米地,你需要從裡面摘選一個棒子最大的玉米。但只能摘一次,而且不能回頭。你第一次走進玉米地,發現很多很好很大的玉米棒子,很快摘下了你看到的第一個比較大的玉米棒子,然後繼續往前走,然而越走越失望,你沮喪地發現前面還有很多比你手裡的大得多的玉米棒子。但是你已經不能夠選擇了。你第二次走進玉米地,同樣也發現了很多很好的玉米棒子,但是這一次你吸取“後悔”的教訓——前面一定有更好的。你一直向前走,直到發現自己差不多走出了玉米地。按照規則,你回不去了。就這樣,你錯過了最好的玉米棒子。
對於在玉米地選擇玉米棒子的問題。數學家的策略是,你要把這片玉米地分成兩個階段。前37%為第一階段。在這個階段,你只看不選,就是認真觀察比較這個階段最大的玉米棒子,記住那個玉米棒子的大小。等過了37%,進入第二階段。從這個階段開始,你一旦遇到一個比第一階段那個最大的玉米棒子還要大的玉米,或者類似的玉米,就毫不猶豫地選擇它。
分兩個階段這個策略和37%這個數字,是數學家歐拉好不容易算出來的,這實際上是一個隨機選擇優化問題。這個辦法就叫37%規則。37%的規則並不能保證你一定能選擇到最大的玉米,但是在這片玉米地里,玉米棒子大小是隨機出現的。在這種隨機出現的情況下,它是一個能夠選到一個足夠大玉米的好辦法。從概率的角度來講,如果你看了不到37%的玉米就開始選擇,你將來很可能後悔選早了;如果你看了超過37%的玉米開始選,你將來可能後悔選晚了。
37%法則的數學過程[2]
假設這片玉米地有N個玉米,數學模型上說,就是先拒掉前面 k 個玉米,不管這些玉米有多大;然後從第 k+1 個玉米開始,一旦看到比之前所有玉米都要大的,就毫不猶豫地選擇它。不難看出,k 的取值很講究,太小了達不到試的效果,太大了又會導致真正可選的餘地不多了。這就變成了一個純數學問題:在玉米總數 n 已知的情況下,當 k 等於何值時,按上述策略選中最大玉米的概率最大?
如何求出最優的 k 值?對於某個固定的 k,如果最適合的玉米出現在了第 i 個位置,k的概率記作P(k)。
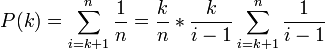
用 x 來表示 k/n 的值,並且假設 n 充分大,則上述公式可以寫成:
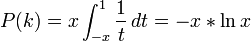
對 -x · ln x 求導,並令這個導數為 0,可以解出 x 的最優值,它就是歐拉研究的神秘常數的倒數—— 1/e
由於 1/e 大約等於 0.37(e ≈2.718281828459),因此這條法則也叫做 37% 法則。
最優停止理論的一個經典案例:秘書問題。
我們在公司中工作,被招聘、面試人都有所經歷,假如你是一個秘書,需要招聘一個人員,篩選了幾分簡歷,決定面試4人,甲、乙、丙、丁。
每次面試之後,你有兩個選擇,要麼聘用此人,要麼拒絕。我們如何才能招聘最佳人選的機會最大,終止面試呢?
我們假設這四個人按照順序丁>丙>乙>甲,我們面試是隨機的,前提也不知道丁是最棒的,如果我們面試完這四個人,是有24種可能的,也就是4種排列。
假如我們有三種策略:
第一種策略:面試完第一人就決定錄用,能錄用到丁的概率是25%;
第二種策略:面試完最後一人就決定錄用(前三人不要),能錄用到丁的概率是25%;
第三種策略:面試完第一人不做決定,作為判定標準,一旦出現比他高的人就錄用,能錄用到丁的概率是46%。
假如第一個人是就是丁,後面面試的能力都比他弱,我們就自行放棄吧,選中丁的概率是為0的;假如第一個人是甲,第二個人能力都比甲好,但是錄取到丁的概率是2/24;假如第一個人是乙,第二個人是甲的話,肯定不用,第二個人是乙、丙、丁就會錄用,但是能錄用到丁的概率就是3/24;假如第一個人是丙,只有丁比他強,因此只要丁一齣現就會被錄取,有6/24的可能性,以上可能性加到一起就是11/24=46%。我們發現第三種策略能選到最優人員的概率要大。
註:以上計算各位可自行搜索,或是自己列一下24個排序,就可以計算出來。
以上是N=4的時候,當N變動時,概率是什麼樣子的呢?
請看下表:
| 人數 | 作為標準的人數 | 選中優秀人員概率 |
| 4 | 1 | 46% |
| 5 | 2 | 43 |
| 6 | 2 | 42.78 |
| ... | ... | ... |
| 100 | 37(37%) | 37.1 |
| 1000 | 369(36.9%) | 36.8 |
當N無限大,我們作為標準的策略就是N/e(e是自然常數),概率就是1/e,是不是很神奇。假如人數是10000,,我們採取的策略是10000/2.71828=3678,不做錄取,只做標準,選中最優人員的概率為1/e=36.8%≈37%。
這就是37%的由來,因此37%是我們在做最優停止時選擇標準根據樣本計算的依據。
比如你打算在18- 40歲之間找到人生的伴侶,那麼按照37%理論來的話,前一段37%也就是 18-26.1歲,用來交往不同的男士,只交往不結婚。等你到了26.1歲的時候,坐下來確定你的“最基本的滿意標準”。然後嫁給一個從那一 天開始你遇到的,第一個好於這個標準的男士,並且不再尋找最優方案。
再比如你想在一個月內買房子,那你可以用37%的時間看房子,確定“最基本滿意標準”,然後從第12天開始,遇見一個好於這個標準的房子,就立即下手。
如果你一生可能要有10段戀愛,那麼找到“那個他”的最大概率發生在拒絕4個戀人之後(代表39.87%的戀愛經歷)。
如果你可能談20段戀愛,則要拒絕前8個人(那個對的人在38.42%處等你)








難以認同,37%法則應該充當參考理論,而不是真理,太拘泥章法反而不好,談戀愛也用參考這,怕不是個憨憨