霍金斯-西蒙條件

出自 MBA智库百科(https://wiki.mbalib.com/)

霍金斯-西蒙條件(Hawkins-Simon Conditions)

　　霍金斯-西蒙條件是指在一個由n個產業部門組成的產業間投入-產出關係的里昂惕夫(Leontief)的系統中。每個產業部門在規模收益不變的條件下生產一種產品，投有聯合產品，並且以固定比例把n個產品作為投入品，產品的供給和需求的平衡可以用一個線性方程系統來表示，即:

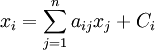　　,(i=1,2,...,n)

　　在這個方程中，a_ij是第j個部門的非負投入繫數，x_j是第j個部門的產出水平、C_i是對第i個產品的最終需求水平。

　　由於投入繫數矩陣A含有第i行和第j列的a_ij產出向量x含有第j列的x_j和最終需求向量C含有第i行的C_i,因此這個系統可以用矩陣方程表示為x=AX+C.

　　如果第j個部門的x_j個非負單位產出被生產出來去滿足正數的最終需求的話，這個系統的生產能力就足以產生超過投入的正的凈產出。這個系統的生產能力等值於-一種條件，即在I是單位矩陣並且有一個使所有元素都是非負的逆矩陣(I − A) ^{− 1}的情況下,n維方陣I-A月要視投入繫數的大小而定，並且完全由後者來決定。如果用約束投入繫數大小的不等式來表述，並且因其發現者的名字(霍金斯和西蒙，)而稱之為霍金斯-西蒙條件，那麼，滿足這種生產能力的必要的和充分的條件就是，矩陣I-A的所有主要主子式必須是正的。

　　由於霍金斯-西蒙條件保證了系統的生產能力，因此，它們是里昂惕夫系統的一個基本的先決條件，而且在把這一條件作為一個內在的正常運轉的子系統包括起來的同時，它們也擴展了系統。它們還使里昂惕夫系統的正常運轉具有動態性質。