辛普森悖論
出自 MBA智库百科(https://wiki.mbalib.com/)
辛普森悖論(Simpson's Paradox)又譯為辛普森詭論
目錄 |
辛普森悖論(Simpson's Paradox)亦有人譯為辛普森詭論,為英國統計學家E.H.辛普森(E.H.Simpson)於1951年提出的悖論,即在某個條件下的兩組數據,分別討論時都會滿足某種性質,可是一旦合併考慮,卻可能導致相反的結論。
例一:一所美國高校的兩個學院,分別是法學院和商學院,新學期招生。人們懷疑這兩個學院有性別歧視。現作如下統計:
法學院
| 性別 | 錄取 | 拒收 | 總數 | 錄取比例 |
|---|---|---|---|---|
| 男生 | 8 | 45 | 53 | 15.1% |
| 女生 | 51 | 101 | 152 | 33.6% |
| 合計 | 59 | 146 | 205 |
商學院
| 性別 | 錄取 | 拒收 | 總數 | 錄取比例 |
|---|---|---|---|---|
| 男生 | 201 | 50 | 251 | 80.1% |
| 女生 | 92 | 9 | 101 | 91.1% |
| 合計 | 293 | 59 | 352 |
根據上面兩個表格來看,女生在兩個學院都被優先錄取。即女生的錄取比率較高。現在將兩學院的數據彙總:
| 性別 | 錄取 | 拒收 | 總數 | 錄取比例 |
|---|---|---|---|---|
| 男生 | 209 | 95 | 304 | 68.8% |
| 女生 | 143 | 110 | 253 | 56.5% |
| 合計 | 352 | 205 | 557 |
在總評中,女生的錄取比率反而比男生低。
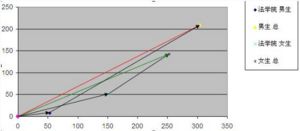
藉助一幅向量圖可以更好的瞭解情況(右圖)這個例子說明,簡單的將分組數據相加彙總,是不能反映真實情況的。
就上述例子說,導致辛普森悖論有兩個前提。
1、兩個分組的錄取率相差很大,就是說法學院錄取率很低,而商學院卻很高。而同時兩種性別的申請者分佈比重相反。女性申請者的大部分分佈在法學院,相反,男性申請者大部分分佈於商學院。結果在數量上來說,拒收率高的法學院拒收了很多的女生,男生雖然有更高的拒收率,但被拒收的 數量卻相對不算多。而錄取率很高的商學院雖然有較高的錄取比例,但是被拒收的男生數量相對法學院來說則明顯較多。
2、有潛在因素影響著錄取情況。就是說,性別並非是錄取率高低的唯一因素,甚至可能是毫無影響的。至於在學院中出現的比率差,可能是隨機事件。又或者是其他因素作用,比如入學成績,卻剛好出現這種錄取比例,使人牽強誤認為這是由性別差異而造成的。
辛普森悖論的迴避[1]
為了避免辛普森悖論出現,就需要斟酌個別分組的權重,以一定的繫數去消除以分組資料基數差異所造成的影響,同時必需瞭解該情境是否存在其他潛在要因而綜合考慮。
辛普森悖論的管理[1]
辛普森悖論就像是欲打100場籃球比賽,然後以總勝率評價好壞,於是有人專找高手挑戰20場而勝1場,另外80場找平手挑戰而勝40場,結果勝率41%,另一人則專挑高手挑戰80場而勝8場,而剩下20場平手打個全勝,結果勝率為28%,比41%小很多,但仔細觀察挑戰對象,後者明顯較有實力。
量與質是不等價的,無奈的是量比質來得容易量測,所以人們總是習慣用量來評定好壞,而此數據卻不是重要的。除了質與量的迷思之外,辛普森悖論的另外一個啟示是:如果我們在人生的抉擇上選擇了一條比較難走的路,就得要有可能不被賞識的領悟,所以這算是懷才不遇這個成語在統計上的詮釋!
評論(共23條)
分組數據彙總時該同化分母:比如純%數據。沒有統一標準的數據是不該統計在一起的--因為結論與論據不在同一個坐標系。餑論只是因果穿越喏坐標系--要沒有矛盾:需要翻譯坐標系。
萵感覺萵有點暈~瞎say
看到這個讓我想到中國的人均住房面積等一系列的人均數據。
有同感
看到這個讓我想到中國的人均住房面積等一系列的人均數據。
我的第一感覺也是中國相關部門的人均面積、人均收入!
因為一個素不相識的人換了個大房子,和自己毛線關係沒有,而據相關部門統計說我人均住房面積增加了,我的生活水平提高了,啊,舉國同慶!
人家工資漲了1千,我的不變,又據相關部門統計說我人均收入增加了,我的生活水平提高了,啊,舉國同慶!
問一下為什麼斜率可以表示錄取率啊?希望你們還在 時隔7年
看到這個讓我想到中國的人均住房面積等一系列的人均數據。
平均數的誤差在於其容易受極值影響,跟辛普森悖論沒關係。








加權啊加權