貝塔繫數
出自 MBA智库百科(https://wiki.mbalib.com/)
貝塔繫數(Beta Coefficient)
目錄 |
貝塔繫數(Beta Coefficient)是一種評估證券系統性風險的工具,用以度量一種證券或一個投資證券組合相對總體市場的波動性。在股票、基金等投資術語中常見。
貝塔繫數是統計學上的概念,它所反映的是某一投資對象相對於大盤的表現情況。其絕對值越大,顯示其收益變化幅度相對於大盤的變化幅度越大;絕對值越小,顯示其變化幅度相對於大盤越小。如果是負值,則顯示其變化的方向與大盤的變化方向相反;大盤漲的時候它跌,大盤跌的時候它漲。由於我們投資於投資基金的目的是為了取得專家理財的服務,以取得優於被動投資於大盤的表現情況,這一指標可以作為考察基金經理降低投資波動性風險的能力。 在計算貝塔繫數時,除了基金的表現數據外,還需要有作為反映大盤表現的指標。
貝塔繫數利用回歸的方法計算。貝塔繫數為1即證券的價格與市場一同變動。貝塔繫數高於1即證券價格比總體市場更波動。貝塔繫數低於1(大於0)即證券價格的波動性比市場為低。
貝塔繫數的計算公式
公式為: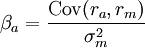
其中Cov(ra,rm)是證券
a 的收益與市場收益的協方差;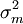 是市場收益的方差。
是市場收益的方差。
因為:
Cov(ra,rm) = ρamσaσm
所以公式也可以寫成:

其中ρam為證券 a 與市場的相關係數;σa為證券 a 的標準差;σm為市場的標準差。
據此公式,貝塔繫數並不代表證券價格波動與總體市場波動的直接聯繫。
不能絕對地說,β越大,證券價格波動(σa)相對於總體市場波動(σm)越大;同樣,β越小,也不完全代表σa相對於σm越小。
甚至即使β = 0也不能代表證券無風險,而有可能是證券價格波動與市場價格波動無關(ρam = 0),但是可以確定,如果證券無風險(σa),β一定為零。
貝塔繫數反映了個股對市場(或大盤)變化的敏感性,也就是個股與大盤的相關性或通俗說的“股性”。可根據市場走勢預測選擇不同的貝塔繫數的證券從而獲得額外收益,特別適合作波段操作使用。當有很大把握預測到一個大牛市或大盤某個大漲階段的到來時,應該選擇那些高貝塔繫數的證券,它將成倍地放大市場收益率,為你帶來高額的收益;相反在一個熊市到來或大盤某個下跌階段到來時,你應該調整投資結構以抵禦市場風險,避免損失,辦法是選擇那些低貝塔繫數的證券。
為避免非系統風險,可以在相應的市場走勢下選擇那些相同或相近貝塔繫數的證券進行投資組合。比如:一支個股貝塔繫數為1.3,說明當大盤漲1%時,它可能漲1.3%,反之亦然;但如果一支個股貝塔繫數為-1.3%時,說明當大盤漲1%時,它可能跌1.3%,同理,大盤如果跌1%,它有可能漲1.3%。
貝塔繫數是反映單個證券或證券組合相對於證券市場系統風險變動程度的一個重要指標。通過對貝塔繫數的計算,投資者可以得出單個證券或證券組合未來將面臨的市場風險狀況.通常貝塔繫數是用歷史數據來計算的,而歷史數據計算出來的貝塔繫數是否具有一定的穩定性,將直接影響貝塔繫數的應用效果。利用CHOW檢驗方法對我國證券市場已經實現股份全流通的上市公司進行檢驗後發現,大部分上市公司在實現股份全流通後,其貝塔繫數並沒有發生顯著的改變,用貝塔繫數進行系統風險的預測可靠性還是相當高的。
本条目由以下用户参与贡献
Angle Roh,苦行者,村姑,山林,Lolo,Zfj3000,Perfecterp,Xiangej,Vulture,Cabbage,Dan,Spilley,essilco.評論(共37條)
貝塔繫數是統計學上的概念,是一個在+1至-1之間的數值, Who says beta is between -1 and 1?
貝塔繫數是統計學上的概念,是一個在+1至-1之間的數值, Who says beta is between -1 and 1?
beta繫數怎麼可能只在-1 和1 之間?
Correlation coefficient is between -1 and +1. Do not mistake it with beta
Correlation coefficient is between -1 and +1. Do not mistake it with beta
right
Beta並不完全代表資產組合的風險與市場風險的比值,而是跟兩者的相關係數有關,因此Beta的大小並不一定說明資產組合的風險相對於市場風險的大小。
謝謝Spilley的修改、補充和完善。
beta繫數怎麼可能只在-1 和1 之間?
他把beta繫數和相關係數搞混了
當然,前提是其他參數不變,僅僅討論Rm變化對beta的影響。
A risk premium is the minimum amount of money by which the expected return on a risky asset must exceed the known return on a risk-free asset, in order to induce an individual to hold the risky asset rather than the risk-free asset. it's not portfolio beta
貝塔繫數是統計學上的概念,是一個在+1至-1之間的數值, Who says beta is between -1 and 1?
統計學的是相關係數,只是貝塔繫數和相關係數的計算公式一樣罷了,但它們所取得對象是不同的。
他把beta繫數和相關係數搞混了
同意..... "beta繫數怎麼可能只在-1 和1 之間? " 此人怎一個2了得....純沒學過數學的..
同問,用BA IIplus的統計工具表計算,算出的beta是0.177,但是公式法算出的是1.5。Rf這裡是0。是不是因為樣本量太少出現的誤差??
各位大神,beta繫數為零所代表的意義是什麼
證券價格波動與市場波動因素無關 但仍有存在風險的可能
各位大神,beta繫數為零所代表的意義是什麼
大盤的走勢特定證券沒有連帶影響








very good!