純策略納什均衡
出自 MBA智库百科(https://wiki.mbalib.com/)
純策略納什均衡（Pure Strategy Nash Equilibrium）
目錄 |
純策略納什均衡是指在一個純策略組合中,如果給定其他的策略不變，該節點不會單方面改變自己的策略，否則不會使節點訪問代價變小。
存在純策略納什均衡的有限次重覆博弈[1]
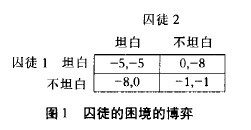
如果重覆博弈中有惟一純策略納什均衡，那麼我們怎麼找出它的純策略納什均衡呢?首先看下麵囚徒的困境的博弈的例子：
我們現在考慮該博弈重覆兩次的重覆博弈，這可以理解成給囚徒兩次坦白機會，最後的得益是兩個階段博弈中各自得益之和．在兩次博弈過程中，雙方知道第一次博弈的結果再進行二次博弈．用逆推歸納法來分析，先分析第二階段，也就是第二次重覆時兩博弈方的選擇．很明顯，這個第二階段仍然是兩囚徒之間的一個囚徒的困境博弈，此時前一階段的結果已成為既成事實，此後又不再有任何的後續階段，因此實現自身當前的最大利益是兩博弈方在該階段決策中的惟一原則．
因此我們不難得出結論，不管前一次的博弈得到的結果如何，第二階段的惟一結果就是原博弈惟一的納什均衡(坦白，坦白)，雙方得益(-5，-5)．
現在再回到第一階段，即第一次博弈．理性的博弈方在第一階段就對後一階段的結局非常清楚，知道第二階段的結果必然是(坦白，坦白)，因此不管第一階段的博弈結果是什麼，雙方在整個重覆博弈中的最終得益，都將是第一階段的基礎上各加-5．因此從第一階段的選擇來看，這個重覆博弈與圖l中得益矩陣表示的一次性博弈實際上是完全等價的．
於是我們可以得出惟一純策略均衡的有限次重覆博弈的結果就是重覆原博弈惟一的純策略納什均衡，這就是這種重覆博弈惟一的子博弈完美納什均衡路徑．
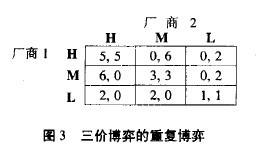
如果重覆博弈中有多個純策略納什均衡，設某一市場有兩個生產同樣質量產品的廠商，他們對產品的定價同有高(H)、中(M)、低(L)三種可能．設高價時市場總利潤為10個單位，中價時市場總利潤為6個單位，低價時市場總利潤為2個單位．再假設兩廠商同時決定價格，價格不等時低價格者獨享利潤，價格相等時雙方平分利潤．這時候兩廠商對價格的選擇就構成了一個靜態博弈問題．我們看一個三價博弈的重覆博弈的例子：
顯然，這個得益矩陣有兩個純策略納什均衡(M，M)和(L，L)，我們也可以看出實際上兩博弈方最大的得益是策略組合(H，H)，但是它並不是納什均衡．現在考慮重覆兩次該博弈，我們採用一種觸發策略(Trigger Strategy)：博弈雙方首先試圖合作，一旦發覺對方不合作也用不合作相報複的策略．使得在第一階段採用(H，H)成為子博弈完美納什均衡，其雙方的策略是這樣的：
博弈方1：第一次選H；如果第一次結果為(H，H)，則第二次選M，如果第一次結果為任何其他策略組合，則第二次選擇L．
博弈方2：同博弈方1．在上述雙方策略組合下，兩次重覆博弈的路徑一定為第一階段(H，H)，第二階段(M，M)，這是一個子博弈完美納什均衡路徑．因為第二階段是一個原博弈的納什均衡，因此不可能有哪一方願意單獨偏離；其次，第一階段的(H，H)雖然不是原來的博弈納什均衡，但是如果一方單獨偏離，採用M能增加1單位得益，這樣的後果卻是第二階段至少要損失2單位的得益，因為雙方採用的是觸發策略，即有報複機制的策略，因此合理的選擇是堅持H．這就說明瞭上述策略組合是這個兩次重覆博弈的子博弈完美納什均衡．
從上述的例子我們可以看出，有多個純策略納什均衡的博弈重覆兩次的子博弈完美納什均衡路徑是，第一階段採用(H，H)，第二階段採用原博弈的納什均衡(M，M)．
如果這個重覆博弈重覆三次，或者更多次，結論也是相似的，仍然用觸發策略，它的子博弈完美納什均衡路徑為除了最後一次以外，每次都採用(H，H)，最後一次採用原博弈的納什均衡(M，M)．
存在純策略納什均衡的無限次重覆博弈[1]
與有限次重覆博弈一樣，無限次重覆博弈也是基本博弈的簡單重覆，但是無限次重覆博弈沒有最後一次重覆，因此無限次重覆博弈與有限次有一些不同．
任何博弈中博弈方策略選擇的依據都是得益的大小，這在重覆博弈中仍然是成立的．但是重覆博弈又與一次性博弈有所不同，因為在重覆博弈中，每一階段都是一個博弈，並且各博弈方都有得益，因此對於重覆博弈，我們要計算的就是博弈結束時的一個總的得益．由於前一次博弈和後一次博弈之間會有損失，因此我們採用一種方法，就是將後一階段的得益折算成當前階段得益的(現在值)的貼現繫數δ．有了貼現繫數δ，那麼在無限次重覆博弈中，某博弈方各階段得益為π1,π2,...,則該博弈方總得益的現在值為：
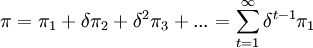
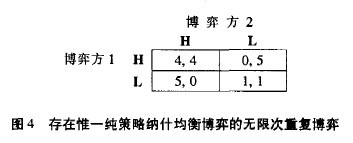
對於存在惟一純策略納什均衡博弈的無限次重覆博弈，我們從下麵的例子來看：
其中博弈方1和博弈方2分別表示兩個廠商，H和L分別表示高價和低價．顯然，該博弈的一次性博弈有惟一的純策略納什均衡(L，L)，但是這個納什均衡並不是最佳策略組合，因為策略組合(H，H)的得益(4，4)比(1，1)要高的多．但是由於(H，H)不是該博弈的納什均衡，所以在一次性博弈中不會被採用．根據上面的分析，此博弈在有限次重覆博弈並不能實現潛在的合作利益，兩博弈方在每次重覆中都不會採用效率較高的(H，H)．為了實現效率較高的合作利益(H，H)，假設兩博弈方都採用觸發策略，也即報複性策略：第一階段採用H，在第t階段，如果前t-l階段的結果都是(H，H)，則繼續採用L．假設博弈方1已經採用了這種策略，現在我們來確定博弈方2在第一階段的最優選擇．如果博弈方2採用L，那麼在第一階段能得到5，但這樣會引起博弈方1一直採用L的報複，自己也只能一直採用L，得益將永遠為1，總得益的現在值為
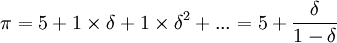
如果博弈方2採用H，則在第一階段他將得4，下一階段又面臨同樣的選擇．若記V為博弈方2在該重覆博弈中每階段都採用最佳選擇的總得益現在值，那麼從第二階段開始的無限次重覆博弈因為與從第一階段開始的只差一 階段，因而在無限次重覆時可看作相同的，其總得益的現在值折算成第一階段的得益為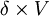
，因此當第一階段的最佳選擇是H時，整個無限次重覆博弈總得益的現在值為
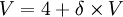或者 
因此，當 
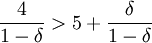解得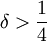
時，博弈方2會採用H策略，否則會採用L策略．也就是說當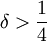時，博弈方2對博弈方1觸發策略的最佳反應是第一階段採用H.這時我們就說雙方採用上述觸發策略是一個納什均衡．
於是我們得出，在有限次重覆博弈中，惟一純策略納什均衡不能實現最大得益(H，H)，而在無限次重覆博弈中，通過觸發策略卻可以實現(H，H)。
暈。