等周定理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　等周定理是指一個幾何中的不等式定理，說明瞭歐幾裡得平面上的封閉圖形的周長以及其面積之間的關係。其中的“等周”指的是周界的長度相等。等周定理說明在周界長度相等的封閉幾何形狀之中，以圓形的面積最大；另一個說法是面積相等的幾何形狀之中，以圓形的周界長度最小。這兩種說法是等價的。它可以以不等式表達：若P為封閉曲線的周界長，A為曲線所包圍的區域面積，。

　　雖然等周定理的結論早已為人所知，但要嚴格的證明這一點並不容易。首個嚴謹的數學證明直到19世紀才出現。之後，數學家們陸續給出了不同的證明，其中有不少是非常簡單的。等周問題有許多不同的推廣，例如在各種曲面而不是平面上的等周問題，以及在高維的空間中給定的“微分幾何|錶面”或區域的最大“邊界長度”問題等。

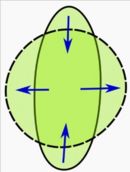
　　在物理中，等周問題和跟所謂的最小作用量原理有關。一個直觀的表現就是水珠的形狀。在沒有外力的情況下（例如失重的太空艙里），水珠的形狀是完全對稱的球體。這是因為當水珠體積一定時，錶面張力會迫使水珠的錶面積達到最小值。根據等周定理，最小值是在水珠形狀為球狀時達到。

　　平面上的等周問題是等周問題最經典的形式，它的出現可以追溯到很早以前。這個問題可以被表述為：在平面上所有周長一定的封閉曲線中，是否有一個圍成的面積最大？如果有的話，是什麼形狀？另一種等價的表述是：當平面上的封閉曲線圍成的面積一定時，怎樣的曲線周長最小？

　　雖然圓看似是問題的錶面答案，但證明此事實其實不易。首個接近答案的步驟出現在1838年——雅各布•史坦納以幾何方法證明若答案存在，答案必然是圓形^[1]。不久之後他的證明被其他數學家完善。

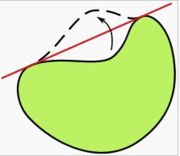
　　其方法包括證明瞭不完全凸的封閉曲線的話，能以翻折凹的部分以成為凸的圖形，以增加面積；不完全對稱的封閉曲線能以傾斜來取得更多的面積。圓，是完全凸和對稱的形狀。可是這些並不足以作為等周定理的嚴格證明。

　　1901年，赫爾維茨憑傅里葉級數和格林定理給出一個純解析的證明。

　　以下給出一個較初等的證明^[2]，分5步。

　　設一條長度為P的封閉曲線圍成的區域的最大面積為A，亦以A、P來標記該區域及其邊界；那麼該圖形應當滿足如下性質：

　　1、A是一個凸區域。

　　 假使不然，A是一個凹區域。那麼根據定義，可以在P內找到兩個點M和N，使其聯機MN有一部份M'N'不包含於A的內部。然而如以M'N'替換掉原來的那段弧，則周長將減少，面積將增加，從而將新圖形擴大若幹倍後得到一個同樣周長，面積比A大的區域。矛盾。

　　2、凡平分周長P的弦必平分面積A。

　　 如果一弦MN平分P而將A分為大小不同的兩部份A₁ > A₂，那麼去掉A₂而將A₁對MN做對稱，則可得到一個周長仍然等於P而面積等於2A₁ > A₁ + A₂ = A的區域，矛盾。

　　3、凡平分A的弦，無論方向，長度相等。

　　 如果不然，不妨設兩弦MN和M'N'均平分面積A而MN>M'N'。那麼分別選取MN及其任一側的曲線（半個P，不妨記為P₁），以及M'N'及其任一側的區域（另行劃分的半個P，記為P'₁），並粘合在一起使得M'N'落在MN上，M與M'重合。

　　 此時，新的圖形仍然滿足周長為P，面積為A的性質，且由於MN>M'N'，N'應落於MN之間。

　　 以M為中心，分別對P₁和P'₁做λ和μ倍的放縮，使兩曲線的終端吻合（即N和N'經過變換之後重合，記為N），得到兩個分別與原區域相似的區域Q₁和Q'₁。適當調整λ和μ的值，使曲線MQ₁NQ'₁M的周長仍為P。

　　 此時Q₁和Q'₁的長度分別等於Pλ / 2和Pμ / 2，所圍的面積分別等於Aλ² / 2和Aμ² / 2；並且由於MN和MN'經過放縮後重合，有λMN = μMN'。

　　 由於曲線MQ₁NQ'₁M的周長仍為P，故Pλ / 2 + Pμ / 2 = P，從而λ + μ = 2；而由λMN = μMN',MN > MN'知0 < λ < 1。

　　 所以，MQ₁NQ'₁M的面積為A(λ² + μ²) / 2 = A(λ² + (2 − λ)²) / 2 = A(λ² − 2λ + 2) > A，與A最大矛盾。

　　4、若MN平分A，O為MN中點，那麼對P上任意一點R，都有OM=ON=OR。

　　 以O為中心，做MRN的中心對稱圖形，R對稱到R'；那麼圖形MR'NRM的周長為P，面積為A。由第3步知MN和RR'的長度應該相等，而O也是RR'的中點，故得結論。

　　5、由於O到P上任意一點的距離都相等，所以P是圓。