等可能性決策法
出自 MBA智库百科(https://wiki.mbalib.com/)
等可能性決策法也稱等可能性法、拉普拉斯決策準則、拉普拉斯方法
目錄 |
等可能性決策是當決策人在決策過程中,不能肯定哪種狀態容易出現,哪種狀態不容易出現時,可以一視同仁,認為各種狀態出現的可能性是相等的。如果有 n個自然狀態,那麼每個自然狀態出現的概率即為 ,然後按收益最大的或損失最小的期望值(或矩陣法)進行決策。這個想法是法國數學家皮埃爾-西蒙·拉普拉斯(Pierre Simon Laplace;1749~1827)首先提出的,所以又叫作拉普拉斯方法。
,然後按收益最大的或損失最小的期望值(或矩陣法)進行決策。這個想法是法國數學家皮埃爾-西蒙·拉普拉斯(Pierre Simon Laplace;1749~1827)首先提出的,所以又叫作拉普拉斯方法。
等可能性決策法是當存在兩種或兩種以上的可行方案時,假定每一種方案遇到各種自然狀態的可能性是相等的,然後求出各種方案的損益期望值,以此作為依據,進行決策;這種決策方法帶有一定的主觀性。
等可能性決策法的主要應用領域:
等可能性決策法主要應用於生產、銷售、建築施工和交通運輸等領域,在決策者無法預測各種自然狀態出現的概率時,認為各種狀態出現的概率相等,但每種狀態下各方案的損益值是可以預測的,在這種情況下,可以使用等可能性決策法。
等可能性決策法的基本操作步驟
以 為各狀態出現的概率,求出方案的期望值 E(A1)如下:
為各狀態出現的概率,求出方案的期望值 E(A1)如下:
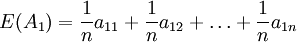
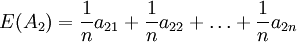

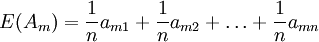
然後取max{E(A1)}(i=1,2,…,m)為決策者的目標值。
若有兩個以上方案的期望值相等,則再比較這些方案的D(A1),D(A1) = E(A1) − min(aij),取 D(A1)值最小的那一個方案。
等可能性決策法的主要應用領域:
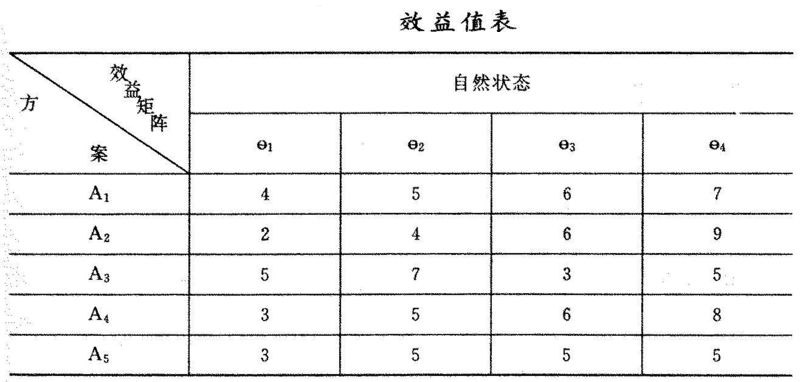
等可能性決策法主要應用於生產、銷售、建築施工和交通運輸等領域,在決策者無法預測各種自然狀態出現的概率時,認為各種狀態出現的概率相等,但每種狀態下各方案的損益值是可以預測的,在這種情況下,可以使用等可能性決策法。4.實用案例今有五個行動方案 A1,A2,A5,四個自然狀態%1,%2,%3,%4(它們出現的概率不知道),其相應的效益值列於下表:
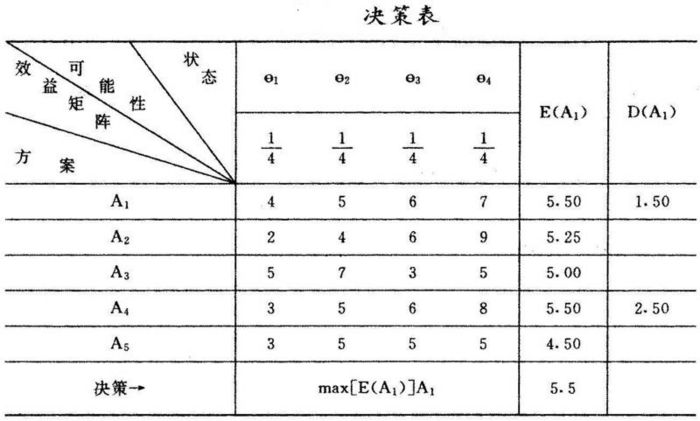
決策表如下: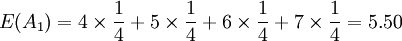
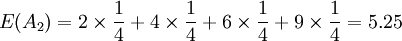
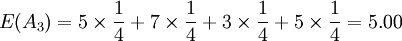
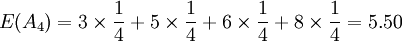
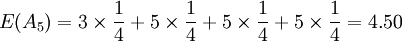
因為 E(A) = E(A4),所以要比較 D(A1)和 D(A4)的大小。
D(A1) = E(A1) − min(aij) = 5.50 − 4 = 1.50
D(A4) = E(A4) − min(a4j) = 5.50 − 3 = 2.50
因為D(A1) < D(A4),所以選取方案 A1。








超有用,謝謝!例子很清晰!