笛沙格定理

出自 MBA智库百科(https://wiki.mbalib.com/)

笛沙格定理(Desargues's theorem)

　　笛沙格定理說明：在射影空間中，有六點A,B,C,a,b,c。Aa,Bb,C,c共點若且唯若AB∩ab,BC∩bc,CA∩ca共線。

　　在射影幾何的對偶性來看，笛沙格定理是自對偶的。

　　笛沙格定理可以表述如下：

　　如果A.a，B.b，C.c共點，則

　　(A.B)∩(a.b)，(A.C)∩(a.c)，(B.C)∩(b.c)共線。

　　利用向量積、數量積和三重積，笛沙格定理也可以表述為：

　　如果

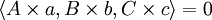
　　那麼

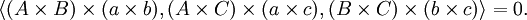
　　向量三重積

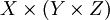
　　等於

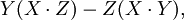
　　我們便可以推出以下的公式

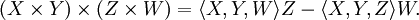
　　從這個公式中，我們可以進一步推出以下的恆等式：

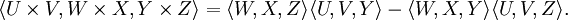
　　利用這個恆等式，笛沙格定理就可以重述為：

　　如果

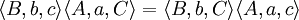
　　那麼

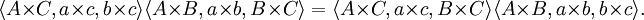
　　把第一個重述的後件再應用上面的恆等式，把三重積交換，並把每一個三重積中的向量進行迴圈置換，我們便得到第二個重述：

　　如果

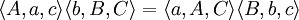
　　那麼

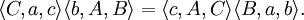
　　註意後件的左端可以從前件的左端通過變數代換A→C，B→A，C→B得到。後件的右端也可以從前件的右端通過變數代換a→c，b→a，c→b得到。

　　向量分析中的一個定理說明，兩個標量三重積的乘積等於以下矩陣的行列式：

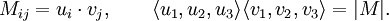
　　把這個定理應用於第二個重述，便得到第三個重述：

　　如果

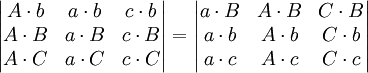
　　那麼

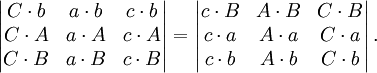
　　把第三個重述中的行列式展開，便得到第四個重述：

　　如果

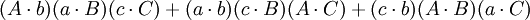
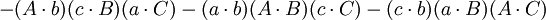
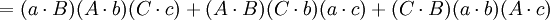
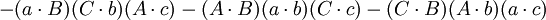
　　那麼

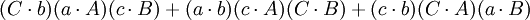
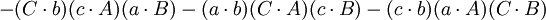
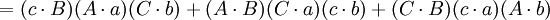
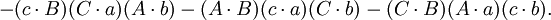
　　第四個重述的兩個方程（前件和後件）的兩端的第一項和第五項都互相抵消，便得到第五個重述：

　　如果

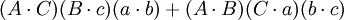
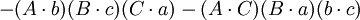
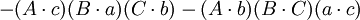
　　那麼

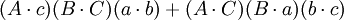
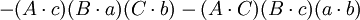
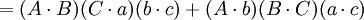
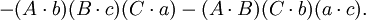
　　在第五個重述的兩個方程之間有八個不同的項；每一個項都出現了兩次。把這些項記為：

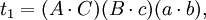
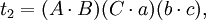
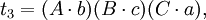
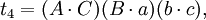
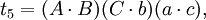
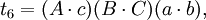
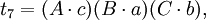
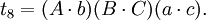
　　於是我們得到第六個重述：

　　如果t₁ + t₂ − t₃ − t₄ = t₅ + t₆ − t₇ − t₈,

　　那麼t₆ + t₄ − t₇ − t₁ = t₂ + t₈ − t₃ − t₅.

　　把前件的右端的項移到左端，再把後件的左端的項移到右端，便得到：

　　如果t₁ + t₂ − t₃ − t₄ − t₅ − t₆ + t₇ + t₈ = 0,那麼

　　0 = t₁ + t₂ − t₃ − t₄ − t₅ − t₆ + t₇ + t₈.

　　這裡可以看出，前件與後件是相同的，因此便證明瞭笛沙格定理。

　　笛沙格定理可以簡單描述為笛沙格圖形 ABC − S − A'B'C'的形式, A,B,C和A',B',C'是三對對應點,S是三對對應點連線的交點.

　　笛沙格定理還可以進行向高維空間的引申, 其引申形式對應的笛沙格圖形為ABCD − S − A'B'C'D', 或者ABCDE − S − A'B'C'D'E', 乃至更高維數的笛沙格圖形.

　　三維空間里的ABCD − S − A'B'C'D'形式的笛沙格定理最有實用價值. 這時,ABCD和A'B'C'D'必須都是四面體, 或至少其中一個是四面體, 另一個為完全四點形; 它們對應線的(組合數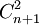, n = 3, 共6個)交點, 也由ABC − S − A'B'C'情況下的共線, 擴展為三維時的共面, 或更一般意義下的"共超平面".

　　基於齊次坐標表示形式對笛沙格定理進行的解析證明是向高維空間作引申時最為簡明方便的證明方式.

　　根據引申的笛沙格定理和基於齊次坐標的表示而定義的幾何變換空間透射其定義涵蓋了理論圖形學中的中心投影,平行投影,平移,反射,位似等幾何變換, 並且可以證明其變換矩陣和矩陣計算理論中的初等矩陣實際上是等價的集合. 該幾何變換的意義主要在於, 圖形學理論中重要的幾何變換或者投影變換的定義及其繫數矩陣的確定可以通過獨立於坐標系選擇的方式進行, 更加簡明和具有一般性意義.