笛沙格定理

出自 MBA智库百科(https://wiki.mbalib.com/)

笛沙格定理(Desargues's theorem)

　　笛沙格定理说明：在射影空间中，有六点A,B,C,a,b,c。Aa,Bb,C,c共点若且唯若AB∩ab,BC∩bc,CA∩ca共线。

　　在射影几何的对偶性来看，笛沙格定理是自对偶的。

　　笛沙格定理可以表述如下：

　　如果A.a，B.b，C.c共点，则

　　(A.B)∩(a.b)，(A.C)∩(a.c)，(B.C)∩(b.c)共线。

　　利用向量积、数量积和三重积，笛沙格定理也可以表述为：

　　如果

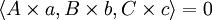
　　那么

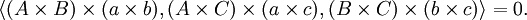
　　向量三重积

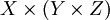
　　等于

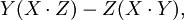
　　我们便可以推出以下的公式

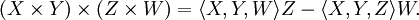
　　从这个公式中，我们可以进一步推出以下的恒等式：

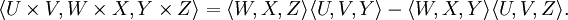
　　利用这个恒等式，笛沙格定理就可以重述为：

　　如果

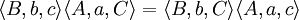
　　那么

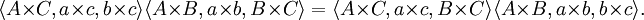
　　把第一个重述的后件再应用上面的恒等式，把三重积交换，并把每一个三重积中的向量进行循环置换，我们便得到第二个重述：

　　如果

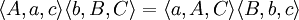
　　那么

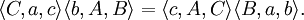
　　注意后件的左端可以从前件的左端通过变量代换A→C，B→A，C→B得到。后件的右端也可以从前件的右端通过变量代换a→c，b→a，c→b得到。

　　向量分析中的一个定理说明，两个标量三重积的乘积等于以下矩阵的行列式：

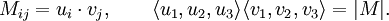
　　把这个定理应用于第二个重述，便得到第三个重述：

　　如果

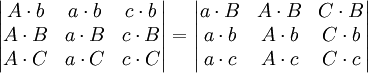
　　那么

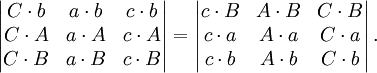
　　把第三个重述中的行列式展开，便得到第四个重述：

　　如果

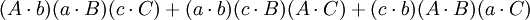
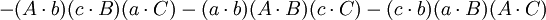
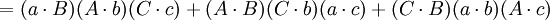
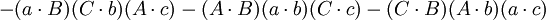
　　那么

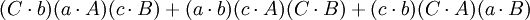
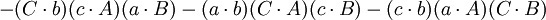
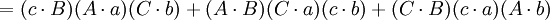
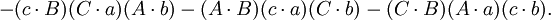
　　第四个重述的两个方程（前件和后件）的两端的第一项和第五项都互相抵消，便得到第五个重述：

　　如果

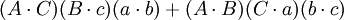
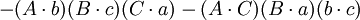
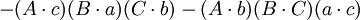
　　那么

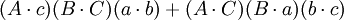
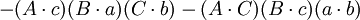
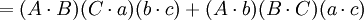
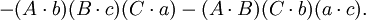
　　在第五个重述的两个方程之间有八个不同的项；每一个项都出现了两次。把这些项记为：

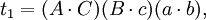
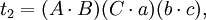
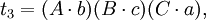
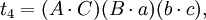
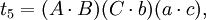
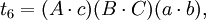
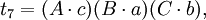
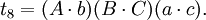
　　于是我们得到第六个重述：

　　如果t₁ + t₂ − t₃ − t₄ = t₅ + t₆ − t₇ − t₈,

　　那么t₆ + t₄ − t₇ − t₁ = t₂ + t₈ − t₃ − t₅.

　　把前件的右端的项移到左端，再把后件的左端的项移到右端，便得到：

　　如果t₁ + t₂ − t₃ − t₄ − t₅ − t₆ + t₇ + t₈ = 0,那么

　　0 = t₁ + t₂ − t₃ − t₄ − t₅ − t₆ + t₇ + t₈.

　　这里可以看出，前件与后件是相同的，因此便证明了笛沙格定理。

　　笛沙格定理可以简单描述为笛沙格图形 ABC − S − A'B'C'的形式, A,B,C和A',B',C'是三对对应点,S是三对对应点连线的交点.

　　笛沙格定理还可以进行向高维空间的引申, 其引申形式对应的笛沙格图形为ABCD − S − A'B'C'D', 或者ABCDE − S − A'B'C'D'E', 乃至更高维数的笛沙格图形.

　　三维空间里的ABCD − S − A'B'C'D'形式的笛沙格定理最有实用价值. 这时,ABCD和A'B'C'D'必须都是四面体, 或至少其中一个是四面体, 另一个为完全四点形; 它们对应线的(组合数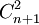, n = 3, 共6个)交点, 也由ABC − S − A'B'C'情况下的共线, 扩展为三维时的共面, 或更一般意义下的"共超平面".

　　基于齐次坐标表示形式对笛沙格定理进行的解析证明是向高维空间作引申时最为简明方便的证明方式.

　　根据引申的笛沙格定理和基于齐次坐标的表示而定义的几何变换空间透射其定义涵盖了理论图形学中的中心投影,平行投影,平移,反射,位似等几何变换, 并且可以证明其变换矩阵和矩阵计算理论中的初等矩阵实际上是等价的集合. 该几何变换的意义主要在于, 图形学理论中重要的几何变换或者投影变换的定义及其系数矩阵的确定可以通过独立于坐标系选择的方式进行, 更加简明和具有一般性意义.