棣莫弗公式

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

棣莫弗公式(De Moivre formula)

什麼是棣莫弗公式

　　棣莫弗公式是指法國數學家棣莫弗（Abraham de Moivre，1667年－1754年）於1707年創立的公式。

　　當一個複數z以極坐標形式表達，即 $z = r (cosθ + i sinθ)$ 時，其 $n$ 次方 $(r (cosθ + i sinθ)) n = r n (cos(n θ) + i sin(n θ))$ ，其中 $n$ 屬於任何整數。

[編輯]

棣莫弗公式的證明

[編輯]

歐拉公式

　　最簡單的方法是應用歐拉公式。

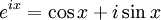
　　 $e^{ix} = \cos x + i\sin x\,$

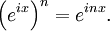
　　 $\left( e^{ix} \right)^n = e^{inx} .$

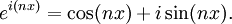
　　 $e^{i(nx)} = \cos (nx) + i\sin (nx).\,$

[編輯]

數學歸納法

[編輯]

正整數情形

　　證明的思路是用數學歸納法證明正整數的情形。

　　設命題為 $P ( n ) = ( \cos \theta + i \sin \theta )^n =\left( \cos n \theta + i \sin n \theta \right), n \in\mathbb{N}$

　　當n=1

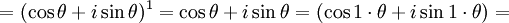　　左式 $= ( \cos \theta + i \sin \theta )^1 = \cos \theta + i \sin \theta = ( \cos 1 \cdot \theta + i \sin 1 \cdot \theta )=$ 右式

　　因此 P(1)成立。

　　假設 $P (k)$ 成立，即 $(cosθ + i sinθ) k = cos(k θ) + i sin(k θ)$

　　當 $n = k + 1$

　　 $\cdot ~~~~~~ (\cos\theta + i\sin\theta)^{k+1}$

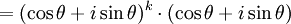
　　 $=(\cos\theta + i\sin\theta)^{k} \cdot (\cos\theta + i\sin\theta)$

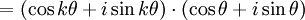
　　 $=(\cos k\theta + i\sin k\theta) \cdot (\cos\theta + i\sin\theta)$

　　 $=(\cos k\theta \cdot \cos\theta + \cos k\theta \cdot i\sin\theta) + (i\sin k\theta \cdot \cos\theta + i\sin k\theta \cdot i\sin\theta)$

　　 $=[\cos k\theta \cdot \cos\theta - \sin k\theta \cdot \sin\theta] + i[\cos k\theta \cdot \sin\theta + \sin k \theta \cdot \cos\theta]$

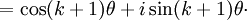
　　 $=\cos (k+1)\theta + i\sin (k+1)\theta \cdot$

　　因此， $P (k + 1)$ 也成立。

　　根據數學歸納法， $\forall n \in \mathbb{N}$ ， $P (n)$ 成立。

[編輯]

負整數情形

　　只需運用恆等式：

　　 $(\cos (n \theta)+i \sin (n \theta)) \cdot (\cos (-n \theta)+i \sin (-n \theta)) =1$ 即可證明。

[編輯]

用棣莫弗公式求根

　　此定理可用來求單位複數的 $n$ 次方根。設 $| z | = 1$ ，表為

　　 $z = cosθ + i sinθ$

　　若 $w n = z$ ，則 $w$ 也可以表成：

　　 $w = cosφ + i sinφ$

　　按照棣莫弗公式：

　　 $w n = (cosφ + i sinφ) n = cos n φ + i sin n φ = cosθ + i sinθ = z$

　　於是得到

　　 $n φ = θ + 2 k π$ （其中 $k \in \Z$ ）

　　也就是：

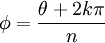
　　 $\phi = \frac{\theta + 2k\pi}{n}$

　　當 $k$ 取 $0, 1, \ldots, n-1$ ，我們得到 $n$ 個不同的根。

取自"https://wiki.mbalib.com/zh-tw/%E6%A3%A3%E8%8E%AB%E5%BC%97%E5%85%AC%E5%BC%8F"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Tracy.

頁面分類: 數學定理

評論(共0條)

提示:評論內容為網友針對條目"棣莫弗公式"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

棣莫弗公式

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是棣莫弗公式

棣莫弗公式的證明

歐拉公式

數學歸納法

正整數情形

負整數情形

用棣莫弗公式求根

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

查看

工具▼

棣莫弗公式

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是棣莫弗公式

棣莫弗公式的證明

歐拉公式

數學歸納法

正整數情形

負整數情形

用棣莫弗公式求根

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈