格拉丘納斯的上下級關係理論
出自 MBA智库百科(https://wiki.mbalib.com/)
法國管理顧問格拉丘納斯(V. A. Graicunas)在1933 年首次發表的一篇論文中,分析了上下級之間可能存在的關係,並提出了一個用來計算在任何管理寬度下,可能存在的人際關係數的數學模型。他的理論把上下級關係分為三種類型:
(一)直接的單一關係。指上級直接地、個別地與其直屬下級發生聯繫。
(二)直接的組合關係。存在於上級與其下屬人員的各種可能組合之間的聯繫。
(三)交叉關係。即下屬彼此打交道的聯繫。
如果A 有三個下屬B、C、 D,那麼他們之間存在的這三種關係如表1 所示。
表1
可能有人會認為類似A→B 和C 與A→C 和B 這樣的關係是一樣的,但格拉丘納斯認為是不同的。因為其中有一個由“以誰為主”的問題所造成的心理狀態。
通過這三種上下級關係的分析,格拉丘納斯認為,在管理寬度的算術級數增加時,主管人員和下屬間可能存在的互相交往的人際關係數幾乎將以幾何級數增加。據此,他提出了一個可以用在任何管理寬度下計算上下級人際關係數目的經驗公式:
C = n[2n − 1 + (n − 1)] 或 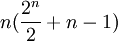
式中,C── 各種可能存在的聯繫總數,即關係數;
N── 一個管理者直接控制的下屬人數,即管理幅度。
當N=1,C=1; N=2,C=6; N=3,C=18; N=10,C=5210
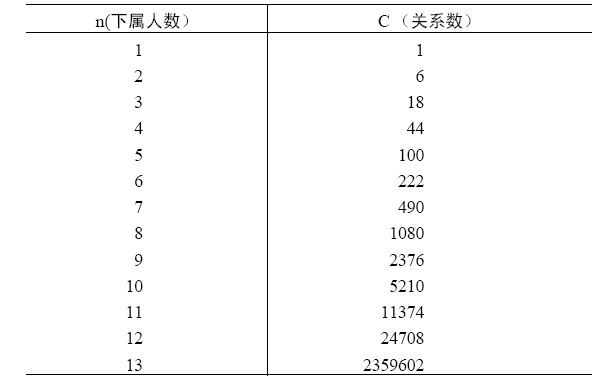
根據這一公式,不同下屬人數的可能關係數可見表2。
表2
由此可見,隨著管理寬度的增加,上下級之間的相互關係數量也在急劇上升。這說明管理較多下屬的複雜性,因此主管人員在增加下屬人數前一定要三思而行。
需要指出的是,格拉丘納斯的這個公式沒有涉及上下級關係發生的頻次和密度,因而它的實用性受到了一走的限制。對一個主管人員來說,相互關係和所發生的頻次和密度(可用所需時間來計算)也應是在確定下屬人數時所考慮的重要因素。
總之,管理幅度受多方面因素的影響,這也決定了管理幅度具有很大的彈性。