因次分析法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

因次分析法（Actor Analysis Method）

什麼是因次分析法

　　因次分析法（Actor Analysis Method）是將各候選方案的成本因素和非成本因素同時加權並加以比較的方法。列舉各種影響因素，將這些因素分為客觀因素和主觀因素兩類，客觀因素能用貨幣來評價，主觀因素是定性的，不能用貨幣表示。確定主觀因素和客觀因素的比重，用以反映主觀因素與客觀因素的相對重要性。確定客觀量度值，再確定主觀評比值和主觀量度值，最後將客觀量度值和主觀量度值進行加權平均，得到位置量度值，即是選址方案的整體評估值，最大者入選。

[編輯]

因次分析法的實施

　　具體實施步驟如下：

　　（1）研究要考慮的各種因素，從中確定哪些因素是必要的。

　　如某一選址無法滿足一項必要因素，應將其刪除。如飲料廠必須依賴水源，就不能考慮缺乏水源的選址。確定必要因素的目的是將不適宜的選址排除在外。

　　（2）將各種必要因素分為客觀因素（成本因素）和主觀因素（非成本因素）兩大類。

　　客觀因素能用貨幣來評價，主觀因素是定性的，不能用貨幣表示。同時要決定主觀因素和客觀因素的比重，用以反映主觀因素與客觀因素的相對重要性。如主觀因素和客觀因素同樣重要，則比重均為0.5。主觀因素的比重值可通過徵詢專家意見決定。

　　（3）確定客觀量度值。

　　對每一可行選址可以找到一個客觀量度值，此值大小受選址的各項成本的影響。其計算方法用數學方程式可表示為：

　　 $C_i=\sum_{j=1}^{M}C_{ij}$

　　 $OM_i=[\frac{C_i\times\sum_{i=1}^{N}}{C_i}]^{-1}$

　　 $C i j$ —i可行位置的第j項成本

　　 $C i$ —第i可行位置的總成本

　　 $O M i$ —第i可行位置的客觀量度值各可行位置的量度值相加，總和必等於1

　　M—客觀因素數目，N為可行位置數.

　　（4）確定主觀評比值。

　　各主觀因素因為沒有一量化值作為比較，所以用強迫選擇法作為衡量各選址優劣的比較。強迫選擇法是將每一選址方案和其他選址方案分別作出成對的比較。令較佳的比重值為1，較差的畢生值則為0。此後，根據各選址方案所得到的比重與總比重的比值來計算該選址的主觀評比值。以數學方程式表示，則為：

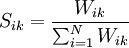
　　 $S_{ik}=\frac{W_{ik}}{\sum_{i=1}^NW_{ik}}$

　　 $S i k$ —i位置對K因素的主觀評比值

　　 $W i k$ —i位置在K因素中的比重；

　　主觀評比值為一量化的比較值。可以利用此數值來比較各選址方案優劣。此數值的變化在0到1之間，愈接近1，則代表選址方案比其他選址方案優越。

　　（5）確定主觀量度值。

　　首先對各主觀因素配上一個重要指數（Ik)。此指數的分配方法可應用(4)中描述的強迫選擇法來確定。然後，再以每因素的主觀評比與該因素的重要指數，分別計算每一可行位置的主量度值（ $S M i$ )。

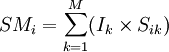
　　 $SM_i=\sum_{k=1}^M(I_k\times S_{ik})$

　　 $S M i$ —i位置的主觀度量值

　　 $I k$ —k主觀因素的重要指數

　　 $S i k$ —i位置對於k因素的評比

　　M—主觀因素的數目.

　　（6）確定位置量度值。

　　位置量度值 $L M i$ 為選址方案的整體評估值，其最大者為最佳選擇方案。其計算方程式為:

　　 $LM_i=X\times(SM_i)+(1-X)\times(OM_i)$

　　 $L M i$ —i位置的位置量度值

　　X—主觀比重值

　　(1-X)—客觀比重值

　　 $S M i$ —i位置的主觀量度值

　　 $O M i$ —i位置的客觀量度值

[編輯]

因次分析法案例分析

[編輯]

案例一:因次分析法在水模型實驗中的應用^[1]

　　一、因次分析在模型實驗中應用的意義

　　假定由流體作用產生的力A的數量和流速v、特征長度l、流體的質量密度ρ和流體的黏滯動力繫數μ有關。此時,怎麼研究上述參量(自變數)和A(依變數)之間的關係呢?換言之,亦即關係式:。

　　註：A——公式

　　註因次分析法——公式

　　通過怎樣的實驗來決定呢?有人可能說:“因為力和上述4個變數有關,為了全部瞭解這一關係式,必須把4個變數一個接一個地變化,而在每次變化的當時保持其餘3個為常數,從而得出F的數值”。

　　這當然可以,但這種辦法是非常原始和費力的,貫徹這種實驗程式需要的時間至少要4倍於真正需要的,因為根據因次理論,上述問題的完全解決僅僅通過一個自變數的變化就可以得到,而且確實是通過任何一個自變數就可以得到,實際上可以選取最容易調節的自變數。從因次理論可以決定:

　　 $F = f (R e)ρ v 212$ 　　(2)

　　式中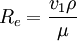， $R_e=\frac{v_1\rho}{\mu}$

　　任何其他的組合形式都是不可能的。所以上述問題的全部解決簡化為函數 $f (R e)$ 的實驗決定。而 $R e$ 的變化,舉例說,僅僅通過v的變化就能實現。雖然只是在一個唯一的實驗設備中用一個唯一的流體進行測試,已經決定的函數f(R_e)和從而得到的表達式 $F = f (R e)ρ v 2 l 2$ 對任何絕對尺寸和所有不同的流體都是有效的。所以說:一個深思熟慮的實驗工作的執行和實驗數據的計算可以放棄因次理論而不用,在今天是不可想象的。

　　二、水模型實驗條件

　　為了瞭解攪拌狀態下氣泡直徑的分佈變化情況,在無槳水模型實驗條件的基礎上,採用不同的槳型和轉動方式對容器內的水溶液進行攪拌。通過改變轉動方式、槳型、液面高度、氣體流量、噴嘴直徑、噴嘴數目、攪拌槳潛入深度以及攪拌轉速等條件研究這些工藝參數對氣泡直徑的影響。

　　三、水模型實驗中不同攪拌參數對氣泡的影響

　　分析氣泡形成過程中影響氣泡脫離尺寸的主要因素。結果表明,攪拌槳型、轉速、轉動方式和氣體流量、噴嘴直徑、噴嘴數目、液面高度、攪拌槳潛入深度、液體黏度等都會影響氣泡的尺寸。在一定物性及一定噴嘴直徑的情況下,氣流量和轉動方式是影響氣泡大小的重要因素,隨著氣流量的增加,氣泡直徑增大;相同條件下,正反轉模式下,得到的氣泡直徑相對較小。噴嘴數目的影響表現得較為複雜,當無槳時,氣泡尺寸隨噴嘴數目的增大而增大;當有槳時,氣泡尺寸隨噴嘴數目的增大而減小,同時由因次分析的替代原則可以發現,為了更好地體現和利用相似準則關係式,噴嘴數目對氣泡平均直徑的影響可以轉換成氣泡出口速度對氣泡平均直徑的影響。

　　通過對實驗數據的分析,可以知道氣泡平均直徑dB主要受以下因素的影響：

　　(1) $d B$ 隨著攪拌轉速n的增加而減小,即 $d_B\infty n^a$ ;

　　(2) $d B$ 隨著氣體流量Q的增加而減小,即 $d_B\infty Q^b$ ;

　　(3) $d B$ 隨著液面高度H的增加而增加,即 $d_B\infty H^c$ ;

　　(4) $d B$ 隨著攪拌槳潛入深度h的增加而增加,即 $d_B\infty h^d$ ;

　　(5) $d B$ 隨著氣體出口速度v的增加而減小,即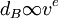 $d_B\infty v^e$ ;

　　(6) $d B$ 隨著噴嘴直徑 $d 0$ 的增加而增加,即 $d_B\infty d^f_0$ ;

　　(7)由^[2]可知d_B隨著入射氣體壓強 $P g$ 的增加而增大,即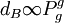 $d_B\infty P^g_g$ ;

　　(8)總結前人對氣泡的研究還發現,氣泡平均直徑也和容器直徑D、氣體密度 $ρ g$ 、氣體黏度 $μ g$ 、氣液錶面張力 $σ g - 1$ 、液體密度 $ρ 1$ 、液體黏度 $μ 1$ 和重力加速度g等因素有關,但它們在實驗中為定值,所以不再討論。

　　由以上分析,利用因次分析法,可以得出一般的函數形式為:。

　　 $d B = f (n, Q, H, h, P g, v, d, D,ρ g,μ g,σ g - 1,ρ 1,μ 1, g)$ 　　(3)

　　或 $f (d B, n, Q, H, h, P g, v, d, D,ρ g,μ g,σ g - 1,ρ 1,μ 1, g) = 0$ 　　(4)

　　諸變數的因次見下表。

　　變數因次表

	d_B	n	Q	H	h	P_g	v	d	D	\rho_2	\mu_2	\sigma_{g-1}	\rho_1	\mu_1	g
M	0	0	0	0	0	1	0	0	0	1	1	1	1	1	0
L	1	0	3	1	1	-1	1	1	1	-3	-1	0	-3	-1	1
T	0	-1	-1	0	0	-2	-1	0	0	0	-1	-2	0	-1	-2

　　四、結合實驗參數建立水模型實驗條件下的因次公式

　　由π定理的分析原理可以知道,總變數數n=15,獨立變數數k=3,可建立n-k=12個無因次組合量。選取\sigma_1、D、v為獨立變數,對於變數d_B、H、h和d_0,它們只含長度因次。因此在構造無因次\Rho時可以直接用獨立變數D表示出來,各個\Rho分別表示為:

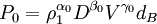　　 $\Rho_0=\rho_1^{\alpha_0}D^{\beta_0}V^{\gamma_0}d_B$ 　　(5)

　　 $\Rho_1=\rho_1^{\alpha_1}D^{\beta_1}V^{\gamma_1}n$ 　　(6)

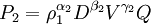　　 $\Rho_2=\rho_1^{\alpha_2}D^{\beta_2}V^{\gamma_2}Q$ 　　(7)

　　 $\Rho_3=\frac{H}{D}$ 　　(8)

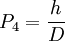　　 $\Rho_4=\frac{h}{D}$ 　　(9)

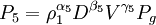　　 $\Rho_5=\rho_1^{\alpha_5}D^{\beta_5}V^{\gamma_5}P_g$ 　　(10)

　　 $\Rho_6=\frac{d_0}{D}$ 　　(11)

　　 $\Rho_7=\rho_1^{\alpha_7}D^{\beta_7}V^{\gamma_7}\rho_g$ 　　(12)

　　 $\Rho_8=\rho_1^{\alpha_8}D^{\beta_8}V^{\gamma_8}\mu_g$ 　　(13)

　　 $\Rho_9=\rho_1^{\alpha_9}D^{\beta_9}V^{\gamma_9}\sigma_{g-1}$ 　　　　(14)

　　 $\Rho_{10}=\rho_1^{\alpha_10}D^{\beta_10}V^{\gamma_10}\mu_1$ 　　(15)

　　 $\Rho_{11}=\rho_1^{\alpha_11}D^{\beta_11}V^{\gamma_11}g$ 　　(16)

　　對於 $Ρ 10$ ,代入諸量的因次可得到因次關係式:

　　 $[M^0L^0T_0]=[ML^{-3}]^{\alpha_0}[L]^{\beta_0}[LT^{-1}]^\gamma_0[L]$ 　　(17)

　　由此可得指數方程組:

　　M 0= $α 0$

　　L 0= $- 3α 0 + β 0 + γ 0$

　　T 0 = $- γ 0$

　　解得 $α 0 = 0,β 0,γ 0 = 0,$ 因此， $\Rho_0=\frac{D_B}{D}$

　　同理,可解出 $Ρ 1$ 到 $Ρ 11$ ,於是可得到:

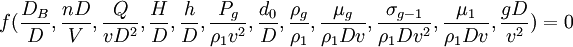　　 $f(\frac{D_B}{D},\frac{nD}{V},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{P_g}{\rho_1v^2},\frac{d_0}{D},\frac{\rho_g}{\rho_1},\frac{\mu_g}{\rho_1Dv},\frac{\sigma_{g-1}}{\rho_1Dv^2},\frac{\mu_1}{\rho_1Dv},\frac{gD}{v^2})=0$ 　　(19)

　　式(16)又可表示成:

　　 $f_1(\frac{D_B}{D},\frac{nD}{V},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},E_u,R_e,W_e,F_r)=0$ 　　(20)

　　為了得到氣泡平均直徑 $d B$ 的表達式,還可以表示為顯函數的形式:

　　 $\frac{D_B}{D}=f_2(\frac{D_B}{D},\frac{nD}{V},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},E_u,R_e,W_e,F_r)$ (21)

　　對於本實驗研究的具體情況來說,根據流體力學的研究結果,對氣泡起主要作用的是 $W e$ 數,即可以忽略 $E u$ 數、 $R e$ 數和 $F r$ 數。

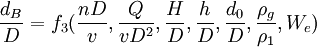　　 $\frac{d_B}{D}=f_3(\frac{nD}{v},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},W_e)$ 　　(22)

　　此外,實驗中 $ρ g$ 和 $ρ 1$ 為定量,於是又可得到:

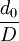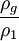　　 $\frac{d_B}{D}=kf_4(\frac{nD}{v},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},W_e)$ 　　(23)

　　 $f_4(\frac{nD}{v},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},W_e)$ 　　(24)

　　隨 $\frac{nD}{v}$ 、 $\frac{Q}{vD^2}$ 、 $\frac{H}{D}$ 、 $\frac{h}{D}$ 、 $\frac{d_0}{D}$ 、 $\frac{\rho_g}{\rho_1}$ 和 $W e$ 數的具體變化關係需要由實驗來確定。

　　根據建立的參數關係式(22)和式(23),結合實驗具體條件,可以推導建立相應的具體經驗公式。根據因次分析的特點,認為不同轉動方式和攪拌槳型下的因次公式的形式是相同的,不同的是具體的經驗公式結果。

　　各種現象的準則關係式在自變數的某一範圍內往往都可以採用冪函數的形式表述,由以上的分析,可以擬合出經驗準則公式為:

　　 $\frac{d_B}{D}=A(\frac{nD}{v})^B(\frac{Q}{vD^2})^C(\frac{h}{D})^D(\frac{d_0}{D})^E(\frac{H}{D})^F(W_e)^G$ 　　(24)

　　其中,A、B、C、D、E、F和G是擬合繫數。

　　將上式兩邊求對數得到:

　　 $\ln\frac{d_B}{D}=\ln A+B\ln\frac{nD}{v}+C\ln\frac{Q}{vD^2}+D\ln\frac{h}{D}+E\ln\frac{d_0}{D}+F\ln\frac{H}{D}+G\ln W_e$ 　　(25)

　　依據以上形式的線性關係,將實驗數據進行處理,就可以得到擬合繫數A、B、C、E、F、F和G。

　　根據對直槳條件下的實驗數據的處理可得到A=0.006 243,B=-0.255 81,C=-0.061 5,D=0.380 53,E=0.113 32,F=-0.158 241,G=-0.082 63。則經驗公式為:

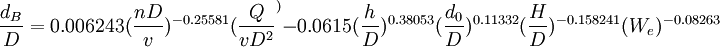　　 $\frac{d_B}{D}=0.006 243(\frac{nD}{v})^{-0.25581}(\frac{Q}{vD^2}^){-0.0615}(\frac{h}{D})^{0.38053}(\frac{d_0}{D})^{0.11332}(\frac{H}{D})^{-0.158241}(W_e)^{-0.08263}$ 在其他條件相同而轉速不同時的值,且由於影響氣泡尺寸的因素眾多,需要對影響氣泡的各個因素進行全面系統的研究。採用相似原理指導下的水模型實驗對各種條件下的氣泡細化的氣泡-熔體兩相流動過程進行研究。利用因次分析法得出相應的經驗公式,為氣泡細化條件下的氣泡直徑的預測提供了參考依據。所完成的主要工作及得到的主要結論如下:

　　(1)通過無槳和有槳水模型實驗中對氣泡直徑的主要影響因素的觀察分析,列舉出具體的影響參數。

　　(2)根據齊次原理和巴金漢定理建立相似準則關係式,然後經過分別整理具體的實驗數據,得出相應的擬合數,從而得出不同實驗條件下的具體的氣泡平均直徑的經驗公式。

　　(3)得出的經驗公式可以為相似條件下的氣泡平均直徑提供預測。

　　(4)經驗公式擬合值與實驗數據吻合良好,誤差在4.2%左右。

　　由於影響氣泡尺寸的因素眾多,需要對影響氣泡的各個因素進行全面系統的研究。採用相似原理指導下的水模型實驗對各種條件下的氣泡細化的氣泡-熔體兩相流動過程進行研究。利用因次分析法得出相應的經驗公式,為氣泡細化條件下的氣泡直徑的預測提供了參考依據。所完成的主要工作及得到的主要結論如下:

　　(1)通過無槳和有槳水模型實驗中對氣泡直徑的主要影響因素的觀察分析,列舉出具體的影響參數。

　　(3)得出的經驗公式可以為相似條件下的氣泡平均直徑提供預測。

　　(4)經驗公式擬合值與實驗數據吻合良好,誤差在4.2%左右。

　　五、數值模擬

n	50	70	100	150	170	180
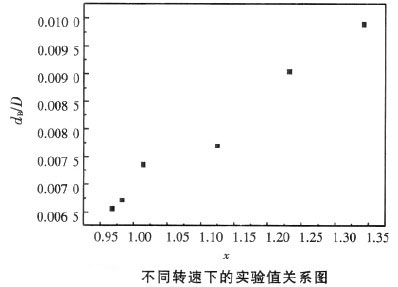
\frac{d_n}{D}	0.00988	0.00904	0.0077	0.00736	0.00671	0.00656
X	1.34309	1.23232	1.12486	1.01404	0.98208	0.96783

　　上表中n為轉速, $d B / D$ 和x均為無因次量。利用上表中的實驗數據可以得到下圖。

　　利用Origin 7.0數據分析軟體可以對實驗得到的經驗公式(24)進行線性擬合,可以得到在同一x下的擬合圖,見下圖。

　　(1)通過無槳和有槳水模型實驗中對氣泡直徑的主要影響因素的觀察分析,列舉出具體的影響參數。

　　(3)得出的經驗公式可以為相似條件下的氣泡平均直徑提供預測。

　　(4)經驗公式擬合值與實驗數據吻合良好,誤差在4.2%左右。

[編輯]

參考文獻

↑ 劉燕,張廷安,王強等.因次分析法在水模型實驗中的應用[J].工業爐,2007,29(6)
↑ 西多連柯.噴粉冶金的理論和實踐[M].田治洲,毛鳳源,譯.北京:冶金工業出版社,1983:10-25

取自"https://wiki.mbalib.com/zh-tw/%E5%9B%A0%E6%AC%A1%E5%88%86%E6%9E%90%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Cabbage,Fghghg.

頁面分類: 選址方法

評論(共0條)

提示:評論內容為網友針對條目"因次分析法"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

因次分析法

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是因次分析法

因次分析法的實施

因次分析法案例分析

案例一:因次分析法在水模型實驗中的應用^[1]

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

查看

工具▼

因次分析法

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是因次分析法

因次分析法的實施

因次分析法案例分析

案例一:因次分析法在水模型實驗中的應用[1]

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

案例一:因次分析法在水模型實驗中的應用^[1]