因次分析法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

因次分析法（Actor Analysis Method）

什么是因次分析法

　　因次分析法（Actor Analysis Method）是将各候选方案的成本因素和非成本因素同时加权并加以比较的方法。列举各种影响因素，将这些因素分为客观因素和主观因素两类，客观因素能用货币来评价，主观因素是定性的，不能用货币表示。确定主观因素和客观因素的比重，用以反映主观因素与客观因素的相对重要性。确定客观量度值，再确定主观评比值和主观量度值，最后将客观量度值和主观量度值进行加权平均，得到位置量度值，即是选址方案的整体评估值，最大者入选。

[编辑]

因次分析法的实施

　　具体实施步骤如下：

　　（1）研究要考虑的各种因素，从中确定哪些因素是必要的。

　　如某一选址无法满足一项必要因素，应将其删除。如饮料厂必须依赖水源，就不能考虑缺乏水源的选址。确定必要因素的目的是将不适宜的选址排除在外。

　　（2）将各种必要因素分为客观因素（成本因素）和主观因素（非成本因素）两大类。

　　客观因素能用货币来评价，主观因素是定性的，不能用货币表示。同时要决定主观因素和客观因素的比重，用以反映主观因素与客观因素的相对重要性。如主观因素和客观因素同样重要，则比重均为0.5。主观因素的比重值可通过征询专家意见决定。

　　（3）确定客观量度值。

　　对每一可行选址可以找到一个客观量度值，此值大小受选址的各项成本的影响。其计算方法用数学方程式可表示为：

　　 $C_i=\sum_{j=1}^{M}C_{ij}$

　　 $OM_i=[\frac{C_i\times\sum_{i=1}^{N}}{C_i}]^{-1}$

　　 $C i j$ —i可行位置的第j项成本

　　 $C i$ —第i可行位置的总成本

　　 $O M i$ —第i可行位置的客观量度值各可行位置的量度值相加，总和必等于1

　　M—客观因素数目，N为可行位置数.

　　（4）确定主观评比值。

　　各主观因素因为没有一量化值作为比较，所以用强迫选择法作为衡量各选址优劣的比较。强迫选择法是将每一选址方案和其他选址方案分别作出成对的比较。令较佳的比重值为1，较差的毕生值则为0。此后，根据各选址方案所得到的比重与总比重的比值来计算该选址的主观评比值。以数学方程式表示，则为：

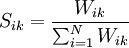
　　 $S_{ik}=\frac{W_{ik}}{\sum_{i=1}^NW_{ik}}$

　　 $S i k$ —i位置对K因素的主观评比值

　　 $W i k$ —i位置在K因素中的比重；

　　主观评比值为一量化的比较值。可以利用此数值来比较各选址方案优劣。此数值的变化在0到1之间，愈接近1，则代表选址方案比其他选址方案优越。

　　（5）确定主观量度值。

　　首先对各主观因素配上一个重要指数（Ik)。此指数的分配方法可应用(4)中描述的强迫选择法来确定。然后，再以每因素的主观评比与该因素的重要指数，分别计算每一可行位置的主量度值（ $S M i$ )。

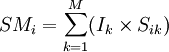
　　 $SM_i=\sum_{k=1}^M(I_k\times S_{ik})$

　　 $S M i$ —i位置的主观度量值

　　 $I k$ —k主观因素的重要指数

　　 $S i k$ —i位置对于k因素的评比

　　M—主观因素的数目.

　　（6）确定位置量度值。

　　位置量度值 $L M i$ 为选址方案的整体评估值，其最大者为最佳选择方案。其计算方程式为:

　　 $LM_i=X\times(SM_i)+(1-X)\times(OM_i)$

　　 $L M i$ —i位置的位置量度值

　　X—主观比重值

　　(1-X)—客观比重值

　　 $S M i$ —i位置的主观量度值

　　 $O M i$ —i位置的客观量度值

[编辑]

因次分析法案例分析

[编辑]

案例一:因次分析法在水模型实验中的应用^[1]

　　一、因次分析在模型实验中应用的意义

　　假定由流体作用产生的力A的数量和流速v、特征长度l、流体的质量密度ρ和流体的黏滞动力系数μ有关。此时,怎么研究上述参量(自变量)和A(依变量)之间的关系呢?换言之,亦即关系式:。

　　注：A——公式

　　注因次分析法——公式

　　通过怎样的实验来决定呢?有人可能说:“因为力和上述4个变量有关,为了全部了解这一关系式,必须把4个变量一个接一个地变化,而在每次变化的当时保持其余3个为常数,从而得出F的数值”。

　　这当然可以,但这种办法是非常原始和费力的,贯彻这种实验程序需要的时间至少要4倍于真正需要的,因为根据因次理论,上述问题的完全解决仅仅通过一个自变量的变化就可以得到,而且确实是通过任何一个自变量就可以得到,实际上可以选取最容易调节的自变量。从因次理论可以决定:

　　 $F = f (R e)ρ v 212$ 　　(2)

　　式中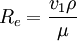， $R_e=\frac{v_1\rho}{\mu}$

　　任何其他的组合形式都是不可能的。所以上述问题的全部解决简化为函数 $f (R e)$ 的实验决定。而 $R e$ 的变化,举例说,仅仅通过v的变化就能实现。虽然只是在一个唯一的实验设备中用一个唯一的流体进行测试,已经决定的函数f(R_e)和从而得到的表达式 $F = f (R e)ρ v 2 l 2$ 对任何绝对尺寸和所有不同的流体都是有效的。所以说:一个深思熟虑的实验工作的执行和实验数据的计算可以放弃因次理论而不用,在今天是不可想象的。

　　二、水模型实验条件

　　为了了解搅拌状态下气泡直径的分布变化情况,在无桨水模型实验条件的基础上,采用不同的桨型和转动方式对容器内的水溶液进行搅拌。通过改变转动方式、桨型、液面高度、气体流量、喷嘴直径、喷嘴数目、搅拌桨潜入深度以及搅拌转速等条件研究这些工艺参数对气泡直径的影响。

　　三、水模型实验中不同搅拌参数对气泡的影响

　　分析气泡形成过程中影响气泡脱离尺寸的主要因素。结果表明,搅拌桨型、转速、转动方式和气体流量、喷嘴直径、喷嘴数目、液面高度、搅拌桨潜入深度、液体黏度等都会影响气泡的尺寸。在一定物性及一定喷嘴直径的情况下,气流量和转动方式是影响气泡大小的重要因素,随着气流量的增加,气泡直径增大;相同条件下,正反转模式下,得到的气泡直径相对较小。喷嘴数目的影响表现得较为复杂,当无桨时,气泡尺寸随喷嘴数目的增大而增大;当有桨时,气泡尺寸随喷嘴数目的增大而减小,同时由因次分析的替代原则可以发现,为了更好地体现和利用相似准则关系式,喷嘴数目对气泡平均直径的影响可以转换成气泡出口速度对气泡平均直径的影响。

　　通过对实验数据的分析,可以知道气泡平均直径dB主要受以下因素的影响：

　　(1) $d B$ 随着搅拌转速n的增加而减小,即 $d_B\infty n^a$ ;

　　(2) $d B$ 随着气体流量Q的增加而减小,即 $d_B\infty Q^b$ ;

　　(3) $d B$ 随着液面高度H的增加而增加,即 $d_B\infty H^c$ ;

　　(4) $d B$ 随着搅拌桨潜入深度h的增加而增加,即 $d_B\infty h^d$ ;

　　(5) $d B$ 随着气体出口速度v的增加而减小,即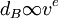 $d_B\infty v^e$ ;

　　(6) $d B$ 随着喷嘴直径 $d 0$ 的增加而增加,即 $d_B\infty d^f_0$ ;

　　(7)由^[2]可知d_B随着入射气体压强 $P g$ 的增加而增大,即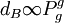 $d_B\infty P^g_g$ ;

　　(8)总结前人对气泡的研究还发现,气泡平均直径也和容器直径D、气体密度 $ρ g$ 、气体黏度 $μ g$ 、气液表面张力 $σ g - 1$ 、液体密度 $ρ 1$ 、液体黏度 $μ 1$ 和重力加速度g等因素有关,但它们在实验中为定值,所以不再讨论。

　　由以上分析,利用因次分析法,可以得出一般的函数形式为:。

　　 $d B = f (n, Q, H, h, P g, v, d, D,ρ g,μ g,σ g - 1,ρ 1,μ 1, g)$ 　　(3)

　　或 $f (d B, n, Q, H, h, P g, v, d, D,ρ g,μ g,σ g - 1,ρ 1,μ 1, g) = 0$ 　　(4)

　　诸变量的因次见下表。

　　变量因次表

	d_B	n	Q	H	h	P_g	v	d	D	\rho_2	\mu_2	\sigma_{g-1}	\rho_1	\mu_1	g
M	0	0	0	0	0	1	0	0	0	1	1	1	1	1	0
L	1	0	3	1	1	-1	1	1	1	-3	-1	0	-3	-1	1
T	0	-1	-1	0	0	-2	-1	0	0	0	-1	-2	0	-1	-2

　　四、结合实验参数建立水模型实验条件下的因次公式

　　由π定理的分析原理可以知道,总变量数n=15,独立变量数k=3,可建立n-k=12个无因次组合量。选取\sigma_1、D、v为独立变量,对于变量d_B、H、h和d_0,它们只含长度因次。因此在构造无因次\Rho时可以直接用独立变量D表示出来,各个\Rho分别表示为:

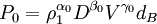　　 $\Rho_0=\rho_1^{\alpha_0}D^{\beta_0}V^{\gamma_0}d_B$ 　　(5)

　　 $\Rho_1=\rho_1^{\alpha_1}D^{\beta_1}V^{\gamma_1}n$ 　　(6)

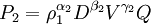　　 $\Rho_2=\rho_1^{\alpha_2}D^{\beta_2}V^{\gamma_2}Q$ 　　(7)

　　 $\Rho_3=\frac{H}{D}$ 　　(8)

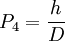　　 $\Rho_4=\frac{h}{D}$ 　　(9)

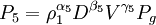　　 $\Rho_5=\rho_1^{\alpha_5}D^{\beta_5}V^{\gamma_5}P_g$ 　　(10)

　　 $\Rho_6=\frac{d_0}{D}$ 　　(11)

　　 $\Rho_7=\rho_1^{\alpha_7}D^{\beta_7}V^{\gamma_7}\rho_g$ 　　(12)

　　 $\Rho_8=\rho_1^{\alpha_8}D^{\beta_8}V^{\gamma_8}\mu_g$ 　　(13)

　　 $\Rho_9=\rho_1^{\alpha_9}D^{\beta_9}V^{\gamma_9}\sigma_{g-1}$ 　　　　(14)

　　 $\Rho_{10}=\rho_1^{\alpha_10}D^{\beta_10}V^{\gamma_10}\mu_1$ 　　(15)

　　 $\Rho_{11}=\rho_1^{\alpha_11}D^{\beta_11}V^{\gamma_11}g$ 　　(16)

　　对于 $Ρ 10$ ,代入诸量的因次可得到因次关系式:

　　 $[M^0L^0T_0]=[ML^{-3}]^{\alpha_0}[L]^{\beta_0}[LT^{-1}]^\gamma_0[L]$ 　　(17)

　　由此可得指数方程组:

　　M 0= $α 0$

　　L 0= $- 3α 0 + β 0 + γ 0$

　　T 0 = $- γ 0$

　　解得 $α 0 = 0,β 0,γ 0 = 0,$ 因此， $\Rho_0=\frac{D_B}{D}$

　　同理,可解出 $Ρ 1$ 到 $Ρ 11$ ,于是可得到:

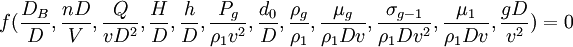　　 $f(\frac{D_B}{D},\frac{nD}{V},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{P_g}{\rho_1v^2},\frac{d_0}{D},\frac{\rho_g}{\rho_1},\frac{\mu_g}{\rho_1Dv},\frac{\sigma_{g-1}}{\rho_1Dv^2},\frac{\mu_1}{\rho_1Dv},\frac{gD}{v^2})=0$ 　　(19)

　　式(16)又可表示成:

　　 $f_1(\frac{D_B}{D},\frac{nD}{V},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},E_u,R_e,W_e,F_r)=0$ 　　(20)

　　为了得到气泡平均直径 $d B$ 的表达式,还可以表示为显函数的形式:

　　 $\frac{D_B}{D}=f_2(\frac{D_B}{D},\frac{nD}{V},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},E_u,R_e,W_e,F_r)$ (21)

　　对于本实验研究的具体情况来说,根据流体力学的研究结果,对气泡起主要作用的是 $W e$ 数,即可以忽略 $E u$ 数、 $R e$ 数和 $F r$ 数。

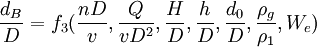　　 $\frac{d_B}{D}=f_3(\frac{nD}{v},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},W_e)$ 　　(22)

　　此外,实验中 $ρ g$ 和 $ρ 1$ 为定量,于是又可得到:

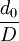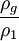　　 $\frac{d_B}{D}=kf_4(\frac{nD}{v},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},W_e)$ 　　(23)

　　 $f_4(\frac{nD}{v},\frac{Q}{vD^2},\frac{H}{D},\frac{h}{D},\frac{d_0}{D},\frac{\rho_g}{\rho_1},W_e)$ 　　(24)

　　随 $\frac{nD}{v}$ 、 $\frac{Q}{vD^2}$ 、 $\frac{H}{D}$ 、 $\frac{h}{D}$ 、 $\frac{d_0}{D}$ 、 $\frac{\rho_g}{\rho_1}$ 和 $W e$ 数的具体变化关系需要由实验来确定。

　　根据建立的参数关系式(22)和式(23),结合实验具体条件,可以推导建立相应的具体经验公式。根据因次分析的特点,认为不同转动方式和搅拌桨型下的因次公式的形式是相同的,不同的是具体的经验公式结果。

　　各种现象的准则关系式在自变量的某一范围内往往都可以采用幂函数的形式表述,由以上的分析,可以拟合出经验准则公式为:

　　 $\frac{d_B}{D}=A(\frac{nD}{v})^B(\frac{Q}{vD^2})^C(\frac{h}{D})^D(\frac{d_0}{D})^E(\frac{H}{D})^F(W_e)^G$ 　　(24)

　　其中,A、B、C、D、E、F和G是拟合系数。

　　将上式两边求对数得到:

　　 $\ln\frac{d_B}{D}=\ln A+B\ln\frac{nD}{v}+C\ln\frac{Q}{vD^2}+D\ln\frac{h}{D}+E\ln\frac{d_0}{D}+F\ln\frac{H}{D}+G\ln W_e$ 　　(25)

　　依据以上形式的线性关系,将实验数据进行处理,就可以得到拟合系数A、B、C、E、F、F和G。

　　根据对直桨条件下的实验数据的处理可得到A=0.006 243,B=-0.255 81,C=-0.061 5,D=0.380 53,E=0.113 32,F=-0.158 241,G=-0.082 63。则经验公式为:

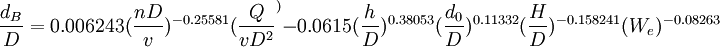　　 $\frac{d_B}{D}=0.006 243(\frac{nD}{v})^{-0.25581}(\frac{Q}{vD^2}^){-0.0615}(\frac{h}{D})^{0.38053}(\frac{d_0}{D})^{0.11332}(\frac{H}{D})^{-0.158241}(W_e)^{-0.08263}$ 在其他条件相同而转速不同时的值,且由于影响气泡尺寸的因素众多,需要对影响气泡的各个因素进行全面系统的研究。采用相似原理指导下的水模型实验对各种条件下的气泡细化的气泡-熔体两相流动过程进行研究。利用因次分析法得出相应的经验公式,为气泡细化条件下的气泡直径的预测提供了参考依据。所完成的主要工作及得到的主要结论如下:

　　(1)通过无桨和有桨水模型实验中对气泡直径的主要影响因素的观察分析,列举出具体的影响参数。

　　(2)根据齐次原理和巴金汉定理建立相似准则关系式,然后经过分别整理具体的实验数据,得出相应的拟合数,从而得出不同实验条件下的具体的气泡平均直径的经验公式。

　　(3)得出的经验公式可以为相似条件下的气泡平均直径提供预测。

　　(4)经验公式拟合值与实验数据吻合良好,误差在4.2%左右。

　　由于影响气泡尺寸的因素众多,需要对影响气泡的各个因素进行全面系统的研究。采用相似原理指导下的水模型实验对各种条件下的气泡细化的气泡-熔体两相流动过程进行研究。利用因次分析法得出相应的经验公式,为气泡细化条件下的气泡直径的预测提供了参考依据。所完成的主要工作及得到的主要结论如下:

　　(1)通过无桨和有桨水模型实验中对气泡直径的主要影响因素的观察分析,列举出具体的影响参数。

　　(3)得出的经验公式可以为相似条件下的气泡平均直径提供预测。

　　(4)经验公式拟合值与实验数据吻合良好,误差在4.2%左右。

　　五、数值模拟

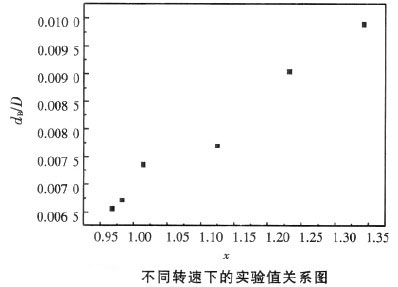
n	50	70	100	150	170	180
\frac{d_n}{D}	0.00988	0.00904	0.0077	0.00736	0.00671	0.00656
X	1.34309	1.23232	1.12486	1.01404	0.98208	0.96783

　　上表中n为转速, $d B / D$ 和x均为无因次量。利用上表中的实验数据可以得到下图。

　　利用Origin 7.0数据分析软件可以对实验得到的经验公式(24)进行线性拟合,可以得到在同一x下的拟合图,见下图。

　　(1)通过无桨和有桨水模型实验中对气泡直径的主要影响因素的观察分析,列举出具体的影响参数。

　　(3)得出的经验公式可以为相似条件下的气泡平均直径提供预测。

　　(4)经验公式拟合值与实验数据吻合良好,误差在4.2%左右。

[编辑]

参考文献

↑ 刘燕,张廷安,王强等.因次分析法在水模型实验中的应用[J].工业炉,2007,29(6)
↑ 西多连柯.喷粉冶金的理论和实践[M].田治洲,毛凤源,译.北京:冶金工业出版社,1983:10-25

来自"https://wiki.mbalib.com/wiki/%E5%9B%A0%E6%AC%A1%E5%88%86%E6%9E%90%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

Cabbage,Fghghg.

页面分类: 选址方法

评论(共0条)

提示:评论内容为网友针对条目"因次分析法"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

因次分析法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是因次分析法

因次分析法的实施

因次分析法案例分析

案例一:因次分析法在水模型实验中的应用^[1]

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

查看

工具箱▼

因次分析法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是因次分析法

因次分析法的实施

因次分析法案例分析

案例一:因次分析法在水模型实验中的应用[1]

参考文献

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

案例一:因次分析法在水模型实验中的应用^[1]