互換裝配法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什麼是互換裝配法^[1]

　　互換裝配法是指在裝配時各配合零件不經任何調整和修配就可以達到裝配精度要求的裝配方法。

[編輯]

互換裝配法的分類^[2]

　　根據互換的程度不同，互換裝配法又分為完全互換裝配法和不完全互換裝配法兩種。

　　(一)完全互換裝配法

　　這種方法的實質是在滿足各環經濟精度的前提下，依靠控制零件的製造精度來保證的。

　　在一般情況下，完全互換裝配法的裝配尺寸鏈按極大極小法計算，即各組成環的公差之和等於或小於封閉環的公差。

　　完全互換裝配法的優點如下：

　　①裝配過程簡單，生產率高；

　　②對工人技術水平要求不高；

　　③便於組織流水作業和實現自動化裝配；

　　④容易實現零部件的專業協作，成本低；

　　⑤便於備件供應及機械維修工作。

　　由於具有上述優點，所以，只要當組成環分得的公差滿足經濟精度要求時，無論何種生產類型都應儘量採用完全互換裝配法進行裝配。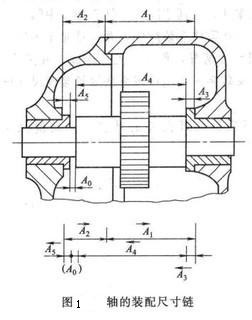

　　例1　　圖1所示的齒輪箱部件，裝配後要求軸向竄動量為0．20～0．70mm，即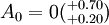 $A_0=0(_{+0.20}^{+0.70})$ mm。已知其他零件的有關基本尺寸 $A 1$ =122mm， $A 2$ =28mm， $A 3$ =5mm， $A 4$ =140mm， $A 5$ =5mm，試決定上、下偏差。

　　解：①畫出裝配尺寸鏈(圖1)，校驗各環基本尺寸。封閉環為

A 0

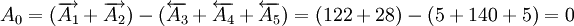，封閉環基本尺寸 $A_0=(\overrightarrow{A_1}+\overrightarrow{A_2})-(\overleftarrow{A_3}+\overleftarrow{A_4}+\overleftarrow{A_5})=(122+28)-(5+140+5)=0$ 　　(mm)

可見各環基本尺寸的給定數值正確。

　　②確定各組成環的公差大小和分佈位置。為了滿足封閉環公差

T 0

=0．50mm的要求，各組成環公差

T i

的累積公差值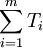 $\sum_{i=1}^m T_i$ 不得超過0．50mm，即應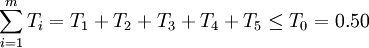 $\sum_{i=1}^m T_i=T_1+T_2+T_3+T_4+T_5\le T_0=0.50$ 　　在最終確定各

T i

值之前，可先按等公差計算分配到各環的平均公差值

T a v . i = T 0 / m = 0.50 / 5 = 0.10

　　(mm)

　　由此值可知，零件的製造精度不算太高，是可以加工的，故用完全互換是可行的。但還應從加工難易和設計要求等方面考慮，調整各組成環公差。比如： $A 1$ 、 $A 2$ 加工難些，公差應略大， $A 3$ 、 $A 5$ 加工方便，則規定可較嚴。故令：

　　 $T 1$ =0．20mm， $T 2$ =0．10mm， $T 3$ =0．05mm

　　再按“單向入體原則”分配公差，如：

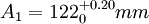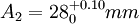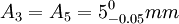
　　 $A_1=122_0^{+0.20}mm$ ， $A_2=28_0^{+0.10}mm$ ， $A_3=A_5=5_{-0.05}^0mm$

　　得中間偏差：

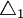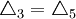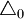　　 $\triangle_1$ =0．10mm， $\triangle_2$ =0．05mm， $\triangle_3=\triangle_5$ =0．025mm， $\triangle_0$ =0．45mm

　　③確定協調環公差的分佈位置。由於

A 4

是特意留下的一個組成環，它的公差大小應在上面分配封閉環公差時，經濟合理地統一決定下來。即：

T 4 = T 0 - T 1 - T 2 - T 3 - T 5 = 0.50 - 0.20 - 0.10 - 0.05 - 0.05 = 0.10

　　(mm) 　　但

T 4

的上、下偏差，須滿足裝配技術條件，因而應通過計算獲得，故稱其為協調環。由於計算結果通常難以滿足標準零件及標準量規的尺寸和偏差值，所以有上述尺寸要求的零件不能選作協調環。

　　協調環

T 4

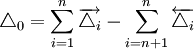
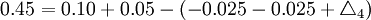
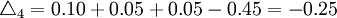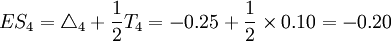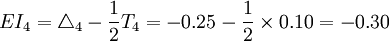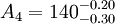的上、下偏差，可參閱圖2計算。代入 $\triangle_0=\sum_{i=1}^n \overrightarrow{\triangle_i}-\sum_{i=n+1}^n \overleftarrow{\triangle_i}$ $0.45=0.10+0.05-(-0.025-0.025+\triangle_4)$ $\triangle_4=0.10+0.05+0.05-0.45=-0.25$ 　　(mm) $ES_4=\triangle_4+\frac{1}{2}T_4=-0.25+\frac{1}{2}\times 0.10=-0.20$ 　　(mm) $EI_4=\triangle_4-\frac{1}{2}T_4=-0.25-\frac{1}{2}\times 0.10=-0.30$ 　　(mm) $A_4=140_{-0.30}^{-0.20}$ 　　(mm) 　　④進行驗算

T 0 = T 1 + T 2 + T 3 + T 4 + T 5 = 0.20 + 0.10 + 0.05 + 0.10 + 0.05 = 0.50

　　(mm)

　　可見，計算符合裝配精度要求。

　　(二)不完全互換裝配法

　　如果裝配精度要求較高，尤其是組成環的數目較多時，若應用極大極小法確定組成環的公差，則組成環的公差將會很小，這樣就很難滿足零件的經濟精度要求。因此，在大批量生產的條件下，就可以考慮不完全互換裝配法，即用概率法解算裝配尺寸鏈。

　　不完全互換裝配法與完全互換裝配法相比，其優點是零件公差可以放大些，從而使零件加工容易、成本低，也能達到互換性裝配的目的。其缺點是將會有一部分產品的裝配精度超差。這就需要採取補救措施或進行經濟論證。

　　現仍以圖1為例進行計算，比較一下各組成環的公差大小。

　　解：①畫出裝配尺寸鏈，校核各環基本尺寸。

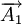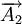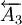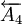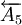　　 $\overrightarrow{A_1}$ 、 $\overrightarrow{A_2}$ 為增環， $\overleftarrow{A_3}$ 、 $\overleftarrow{A_4}$ 、 $\overleftarrow{A_5}$ 為減環，封閉環為

A 0

，封閉環的基本尺寸為 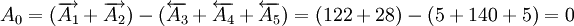$A_0=(\overrightarrow{A_1}+\overrightarrow{A_2})-(\overleftarrow{A_3}+\overleftarrow{A_4}+\overleftarrow{A_5})=(122+28)-(5+140+5)=0$ 　　(mm)

　　②確定各組成環尺寸的公差大小和分佈位置

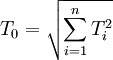　　由於用概率法解算，所以， $T_0=\sqrt{\sum_{i=1}^n T_i^2}$ ，在最終確定各

T i

值之前，也按等公差計算各環的平均公差值 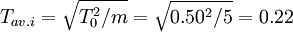$T_{av.i}=\sqrt{T_0^2/m}=\sqrt{0.50^2/5}=0.22$ 　　(mm)

　　按加工難易的程度，參照上值調整各組成環公差值如下

　　 $T 1$ =0．40mm， $T 2$ =0．20mm， $T 3 = T 5$ =0．08mm

　　為滿足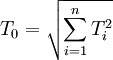 $T_0=\sqrt{\sum_{i=1}^n T_i^2}$ 的要求，應從協調環公差進行計算

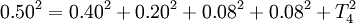
　　 $0.50^2=0.40^2+0.20^2+0.08^2+0.08^2+T_4^2$

　　 $T 4$ =0．192mm

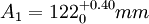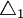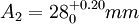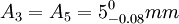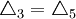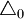　　按“單向入體原則”分配公差，取 $A_1=122_0^{+0.40}mm$ ， $\triangle_1$ =0.20mm， $A_2=28_0^{+0.20}mm$ ， $\triangle_2$ =0.10mm $A_3=A_5=5_{-0.08}^0mm$ ， $\triangle_3=\triangle_5$ =-0.40mm， $\triangle_0$ =0.45mm

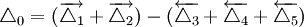
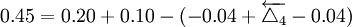
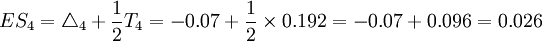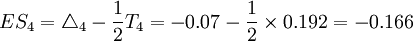　　③定協調環公差的分佈位置 $\triangle_0=(\overrightarrow{\triangle_1}+\overrightarrow{\triangle_2})-(\overleftarrow{\triangle_3}+\overleftarrow{\triangle_4}+\overleftarrow{\triangle_5})$ $0.45=0.20+0.10-(-0.04+\overleftarrow{\triangle_4}-0.04)$ $\overleftarrow{\triangle_4}=0.20+0.10+0.08-0.45=-0.07$ 　　(mm) $ES_4=\triangle_4+\frac{1}{2}T_4=-0.07+\frac{1}{2}\times 0.192=-0.07+0.096=0.026$ 　　(mm) $ES_4=\triangle_4-\frac{1}{2}T_4=-0.07-\frac{1}{2}\times 0.192=-0.166$ 　　(mm) $A_4=140_{-0.166}^{+0.026}$ 　　(mm)

[編輯]

參考文獻

↑ 餘承輝,薑晶主編.第七章機械裝配工藝基礎機械製造工藝與夾具.上海科學技術出版社,2010.07.
↑ 倪森壽主編.第九章機械裝配工藝基礎機械製造工藝與裝備.化學工業出版社,2009.3.

取自"https://wiki.mbalib.com/zh-tw/%E4%BA%92%E6%8D%A2%E8%A3%85%E9%85%8D%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

连晓雾.

頁面分類: 機械 | 設備管理

評論(共0條)

提示:評論內容為網友針對條目"互換裝配法"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

互換裝配法

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是互換裝配法^[1]

互換裝配法的分類^[2]

相關條目

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

查看

工具▼

互換裝配法

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是互換裝配法[1]

互換裝配法的分類[2]

相關條目

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

什麼是互換裝配法^[1]

互換裝配法的分類^[2]