互换装配法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什么是互换装配法^[1]

　　互换装配法是指在装配时各配合零件不经任何调整和修配就可以达到装配精度要求的装配方法。

[编辑]

互换装配法的分类^[2]

　　根据互换的程度不同，互换装配法又分为完全互换装配法和不完全互换装配法两种。

　　(一)完全互换装配法

　　这种方法的实质是在满足各环经济精度的前提下，依靠控制零件的制造精度来保证的。

　　在一般情况下，完全互换装配法的装配尺寸链按极大极小法计算，即各组成环的公差之和等于或小于封闭环的公差。

　　完全互换装配法的优点如下：

　　①装配过程简单，生产率高；

　　②对工人技术水平要求不高；

　　③便于组织流水作业和实现自动化装配；

　　④容易实现零部件的专业协作，成本低；

　　⑤便于备件供应及机械维修工作。

　　由于具有上述优点，所以，只要当组成环分得的公差满足经济精度要求时，无论何种生产类型都应尽量采用完全互换装配法进行装配。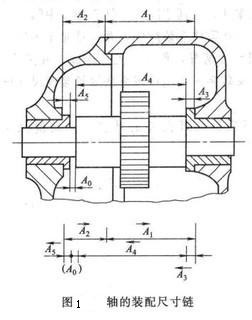

　　例1　　图1所示的齿轮箱部件，装配后要求轴向窜动量为0．20～0．70mm，即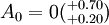 $A_0=0(_{+0.20}^{+0.70})$ mm。已知其他零件的有关基本尺寸 $A 1$ =122mm， $A 2$ =28mm， $A 3$ =5mm， $A 4$ =140mm， $A 5$ =5mm，试决定上、下偏差。

　　解：①画出装配尺寸链(图1)，校验各环基本尺寸。封闭环为

A 0

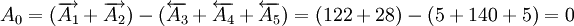，封闭环基本尺寸 $A_0=(\overrightarrow{A_1}+\overrightarrow{A_2})-(\overleftarrow{A_3}+\overleftarrow{A_4}+\overleftarrow{A_5})=(122+28)-(5+140+5)=0$ 　　(mm)

可见各环基本尺寸的给定数值正确。

　　②确定各组成环的公差大小和分布位置。为了满足封闭环公差

T 0

=0．50mm的要求，各组成环公差

T i

的累积公差值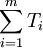 $\sum_{i=1}^m T_i$ 不得超过0．50mm，即应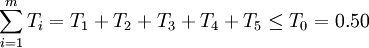 $\sum_{i=1}^m T_i=T_1+T_2+T_3+T_4+T_5\le T_0=0.50$ 　　在最终确定各

T i

值之前，可先按等公差计算分配到各环的平均公差值

T a v . i = T 0 / m = 0.50 / 5 = 0.10

　　(mm)

　　由此值可知，零件的制造精度不算太高，是可以加工的，故用完全互换是可行的。但还应从加工难易和设计要求等方面考虑，调整各组成环公差。比如： $A 1$ 、 $A 2$ 加工难些，公差应略大， $A 3$ 、 $A 5$ 加工方便，则规定可较严。故令：

　　 $T 1$ =0．20mm， $T 2$ =0．10mm， $T 3$ =0．05mm

　　再按“单向入体原则”分配公差，如：

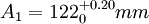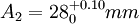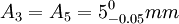
　　 $A_1=122_0^{+0.20}mm$ ， $A_2=28_0^{+0.10}mm$ ， $A_3=A_5=5_{-0.05}^0mm$

　　得中间偏差：

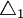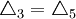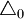　　 $\triangle_1$ =0．10mm， $\triangle_2$ =0．05mm， $\triangle_3=\triangle_5$ =0．025mm， $\triangle_0$ =0．45mm

　　③确定协调环公差的分布位置。由于

A 4

是特意留下的一个组成环，它的公差大小应在上面分配封闭环公差时，经济合理地统一决定下来。即：

T 4 = T 0 - T 1 - T 2 - T 3 - T 5 = 0.50 - 0.20 - 0.10 - 0.05 - 0.05 = 0.10

　　(mm) 　　但

T 4

的上、下偏差，须满足装配技术条件，因而应通过计算获得，故称其为协调环。由于计算结果通常难以满足标准零件及标准量规的尺寸和偏差值，所以有上述尺寸要求的零件不能选作协调环。

　　协调环

T 4

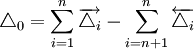
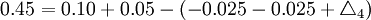
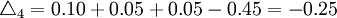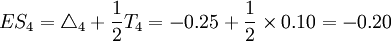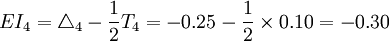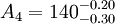的上、下偏差，可参阅图2计算。代入 $\triangle_0=\sum_{i=1}^n \overrightarrow{\triangle_i}-\sum_{i=n+1}^n \overleftarrow{\triangle_i}$ $0.45=0.10+0.05-(-0.025-0.025+\triangle_4)$ $\triangle_4=0.10+0.05+0.05-0.45=-0.25$ 　　(mm) $ES_4=\triangle_4+\frac{1}{2}T_4=-0.25+\frac{1}{2}\times 0.10=-0.20$ 　　(mm) $EI_4=\triangle_4-\frac{1}{2}T_4=-0.25-\frac{1}{2}\times 0.10=-0.30$ 　　(mm) $A_4=140_{-0.30}^{-0.20}$ 　　(mm) 　　④进行验算

T 0 = T 1 + T 2 + T 3 + T 4 + T 5 = 0.20 + 0.10 + 0.05 + 0.10 + 0.05 = 0.50

　　(mm)

　　可见，计算符合装配精度要求。

　　(二)不完全互换装配法

　　如果装配精度要求较高，尤其是组成环的数目较多时，若应用极大极小法确定组成环的公差，则组成环的公差将会很小，这样就很难满足零件的经济精度要求。因此，在大批量生产的条件下，就可以考虑不完全互换装配法，即用概率法解算装配尺寸链。

　　不完全互换装配法与完全互换装配法相比，其优点是零件公差可以放大些，从而使零件加工容易、成本低，也能达到互换性装配的目的。其缺点是将会有一部分产品的装配精度超差。这就需要采取补救措施或进行经济论证。

　　现仍以图1为例进行计算，比较一下各组成环的公差大小。

　　解：①画出装配尺寸链，校核各环基本尺寸。

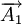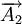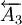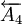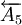　　 $\overrightarrow{A_1}$ 、 $\overrightarrow{A_2}$ 为增环， $\overleftarrow{A_3}$ 、 $\overleftarrow{A_4}$ 、 $\overleftarrow{A_5}$ 为减环，封闭环为

A 0

，封闭环的基本尺寸为 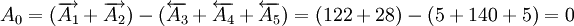$A_0=(\overrightarrow{A_1}+\overrightarrow{A_2})-(\overleftarrow{A_3}+\overleftarrow{A_4}+\overleftarrow{A_5})=(122+28)-(5+140+5)=0$ 　　(mm)

　　②确定各组成环尺寸的公差大小和分布位置

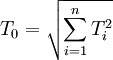　　由于用概率法解算，所以， $T_0=\sqrt{\sum_{i=1}^n T_i^2}$ ，在最终确定各

T i

值之前，也按等公差计算各环的平均公差值 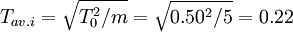$T_{av.i}=\sqrt{T_0^2/m}=\sqrt{0.50^2/5}=0.22$ 　　(mm)

　　按加工难易的程度，参照上值调整各组成环公差值如下

　　 $T 1$ =0．40mm， $T 2$ =0．20mm， $T 3 = T 5$ =0．08mm

　　为满足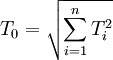 $T_0=\sqrt{\sum_{i=1}^n T_i^2}$ 的要求，应从协调环公差进行计算

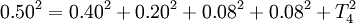
　　 $0.50^2=0.40^2+0.20^2+0.08^2+0.08^2+T_4^2$

　　 $T 4$ =0．192mm

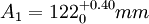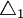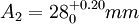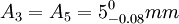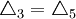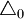　　按“单向入体原则”分配公差，取 $A_1=122_0^{+0.40}mm$ ， $\triangle_1$ =0.20mm， $A_2=28_0^{+0.20}mm$ ， $\triangle_2$ =0.10mm $A_3=A_5=5_{-0.08}^0mm$ ， $\triangle_3=\triangle_5$ =-0.40mm， $\triangle_0$ =0.45mm

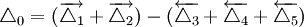
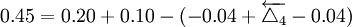
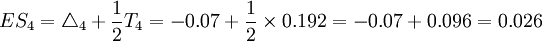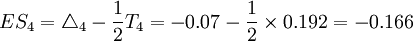　　③定协调环公差的分布位置 $\triangle_0=(\overrightarrow{\triangle_1}+\overrightarrow{\triangle_2})-(\overleftarrow{\triangle_3}+\overleftarrow{\triangle_4}+\overleftarrow{\triangle_5})$ $0.45=0.20+0.10-(-0.04+\overleftarrow{\triangle_4}-0.04)$ $\overleftarrow{\triangle_4}=0.20+0.10+0.08-0.45=-0.07$ 　　(mm) $ES_4=\triangle_4+\frac{1}{2}T_4=-0.07+\frac{1}{2}\times 0.192=-0.07+0.096=0.026$ 　　(mm) $ES_4=\triangle_4-\frac{1}{2}T_4=-0.07-\frac{1}{2}\times 0.192=-0.166$ 　　(mm) $A_4=140_{-0.166}^{+0.026}$ 　　(mm)

[编辑]

参考文献

↑ 余承辉,姜晶主编.第七章机械装配工艺基础机械制造工艺与夹具.上海科学技术出版社,2010.07.
↑ 倪森寿主编.第九章机械装配工艺基础机械制造工艺与装备.化学工业出版社,2009.3.

来自"https://wiki.mbalib.com/wiki/%E4%BA%92%E6%8D%A2%E8%A3%85%E9%85%8D%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

连晓雾.

页面分类: 机械 | 设备管理

评论(共0条)

提示:评论内容为网友针对条目"互换装配法"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

互换装配法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是互换装配法^[1]

互换装配法的分类^[2]

相关条目

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

查看

工具箱▼

互换装配法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是互换装配法[1]

互换装配法的分类[2]

相关条目

参考文献

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

什么是互换装配法^[1]

互换装配法的分类^[2]