KMRW声誉模型
出自 MBA智库百科(https://wiki.mbalib.com/)
KMRW声誉模型(KMRW Reputation Model)
目录 |
KMRW声誉模型有时也称KMRW模型“四人帮模型”,是由戴维·M·克雷普斯(David M.Kreps)、保罗·米格罗姆(Paul Milgrom)、约翰·罗伯茨(John Roberts)和罗伯特·威尔逊 (Robert Wilson)所建立的。
KMRW声誉模型证明,参与人对其他参与人支付函数或战略空间的不完全信息对均衡结果有重要影响,合作行为在有限次重复博弈中会出现,只要博弈重复次数足够长。
KMRW声誉模型对有限重复博弈中信誉效应(既合作现象)做出了很好的解释。
在完全信息情况下,不论博弈重复多少次,只要重复的次数是有限的,唯一的子博弈精炼纳什均衡是每个参与人在每次博弈中选择静态均衡战略(假定静态博弈的纳什均衡是唯一的),即有限次重复不可能导致参与人的合作行为。特别地,在有限次重复囚徒博弈中,每次都选择“坦白”是每个囚徒的最优战略。 这一结果似乎与人们的直观感觉不一致。阿克赛尔罗德(Axelrod,1981和1984年)的锦标赛实验结果表明,在200次有限次重复囚徒博弈中,合作行为频繁出现,而“针锋相对”战略是最稳健的战略。
“理什囚徒”只是对我们已经熟悉的“囚徒”及其行为的一个简单化概括,这里可以理解为机会主义者,或者非合作型参与人; “非理性囚徒”是对具有不同于我们熟悉的行为方式的另一类囚徒的概括,这里可以理解为讲义气重信誉的人,或者合作型参与人
他们证明,参与人对其他参与人支付函数或战略空间的不完全信息对均衡结果有重要影响,只要博弈重复的次数足够多,合作行为在有限次重复博弈中就会出现。在其模型中,囚徒博弈中的每个参与人并不知道对方的类型,即是“理性的”,还是“非理性的”,非理性的交易方只选择触发策略。每个参与人对自己类型的了解属于私有信息,只知道对方属于非理性的概率为P。在此条件下,在T阶段重复囚徒博弈中,如果每个囚徒都有P>0的概率是非理性的(即只选择“针锋相对”或“冷酷战略”),如果T足够大,n那么存在一个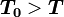 ,使得下列战略组合构成一个精炼贝叶斯均衡:
所有理性囚徒在
,使得下列战略组合构成一个精炼贝叶斯均衡:
所有理性囚徒在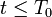 阶段选择合作(抵赖),在
阶段选择合作(抵赖),在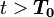 阶段选择不合作(坦白);并且,非合作阶段的数量
阶段选择不合作(坦白);并且,非合作阶段的数量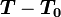 只与p有关,而与T无关。
只与p有关,而与T无关。
Kreps等人的思想后来被总结为KMRW定理。KWRM定理的一个直观解释是(张维迎,1996),每一个参与人尽管在选择合作时可能面临被对手出卖的风险(从而可能得到一个较低的现阶段支付),若对方是合作类型的话,如果他选择不合作,就暴露了自己是非合作型的,从而失去了获得长期合作收益的可能。只要博弈重复的次数足够多,未来收益的损失就超过短期被出卖的损失。因此,即使他们在本性上并不是合作型的,在博弈开始时每一个参与人都想树立一个合作形象(使对方认为自己是喜欢合作的),而只有在博弈快结束时,参与人一次性地把自己过去建立的声誉用尽,合作才会停止(因为此时,短期收益很大而未来损失很小)。该模型的出色解释力在于,大量的事实表明,将参与人外生的具有合作倾向假定并非合理,大多数的合作发生于对自身利益的考虑。在一些长期的交易关系中,交易各方都会致力于建立形象和维护声誉,虽然这些声誉在短期来看并非是经济的,但长期的合作收入流的补偿却表明这种声誉的建立是最优的选择。
Klein(1997)更加明确地指出,现代社会复制声誉的主要手段是现代组织,包括企业组织、社团组织(如宗教团体,商会),以及大量的中介组织。Tadelis(1999)认为声誉是企业一项重要的无形资产,它附属于企业的名称并由其展现 。在他的模型中,企业唯一的资产是与企业声誉相联系的企业名称,对企业名称的交易就等于企业声誉的交易。
在T阶段重复囚徒博弈中,如果每个囚徒都有P>0的概率是非理性的(即只选择“针锋相对”或“冷酷战略”),如果T足够大,n那么存在一个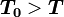 ,使得下列战略组合构成一个精炼贝叶斯均衡:
所有理性囚徒在
,使得下列战略组合构成一个精炼贝叶斯均衡:
所有理性囚徒在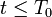 阶段选择合作(抵赖),在
阶段选择合作(抵赖),在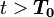 阶段选择不合作(坦白);并且,非合作阶段的数量
阶段选择不合作(坦白);并且,非合作阶段的数量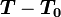 只与p有关,而与T无关。
只与p有关,而与T无关。
KMRW 模型中有以下几点需要强调:
(1)KMRW分析主要适应于多阶段重复博弈。并且信息是不对称的,参与人是非完全理性的;
(2)KMRW模型的出发点。只要阶段博弈重复次数足够多。参与人有足够的耐心。即使P非常小,这种小小的不确定性也对参与人有着较大的影响;
(3)Kreps等人对序贯均衡证明了在T阶段重复博弈中,如果存在P>0的概率。参与人是非理性的(即只采取针锋相对策略或冷酷策略),如果T够大.任何一个参与人选择背叛的阶段数是存在着一个上限的。这个上限依赖于P及阶段博弈的盈利而与T无关,即参与人在相当多的阶段存在着合作;
(4)如果对阶段博弈的盈利即P强加上若干条件,参与人对针锋相对策略的最优反应将是合作下去直到博弈的最后一个阶段。
尽管每一个囚徒在选择合作时冒着被其他囚徒出卖的风险(从而可能得到一个较低的现阶段支付),但如果他选择不合作,就暴露了自己是非合作型的,从而失去了获得长期合作收益的可能,如果对方是合作型的话;
如果博弈重复的次数足够多,未来收益的损失就超过了短期被出卖的损失,因此,在博弈的开始,每一个参与人都想树立一个合作形象(使对方认为自己是喜欢合作的),即使他在本性上并不是合作型的;
只有在博弈快结束的时候,参与人才会一次性地把自己的过去建立的声誉利用尽,合作才会停止,因为此时,短其收益很大而未来损失很小;
KMRW定理解释了“大智若愚”,这里,智者囚徒博弈中的理性囚徒(非合作型),“愚者”即囚徒博弈中的非理性囚徒(合作型)。 在许多情况下,大智若愚确实是“智者”追求自己利益的最佳方式。
只要博弈重复的次数足够长,参与人有足够的耐心(只要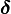 足够接近于1),即使(有关参与人类型的)小小的不确定性,也可能引起均衡结果的重大改变(很小的p就可以保证合作均衡的出现,但如果p=0,合作均衡不可能出现)。 当然,合作均衡的可能性依赖于我们有关非理性参与人行为的假定。比如,如果我们假定,不论对方选择什么,非理性囚徒总是选择D(合作),那么,合作均衡就不会出现,因为,给定非理性囚徒总是选择D的情况下,C是理性囚徒的占优战略。如果不论你如何损害对方的利益,对方总是“以德报怨”、"仇将恩报"。
足够接近于1),即使(有关参与人类型的)小小的不确定性,也可能引起均衡结果的重大改变(很小的p就可以保证合作均衡的出现,但如果p=0,合作均衡不可能出现)。 当然,合作均衡的可能性依赖于我们有关非理性参与人行为的假定。比如,如果我们假定,不论对方选择什么,非理性囚徒总是选择D(合作),那么,合作均衡就不会出现,因为,给定非理性囚徒总是选择D的情况下,C是理性囚徒的占优战略。如果不论你如何损害对方的利益,对方总是“以德报怨”、"仇将恩报"。
KWRW模型解开了有限重复博弈的悖论,但也带来了均衡的多重性问题。 弗登伯格和马司肯(1986年)证明,类似完全信息无限重复博弈的“无名氏定理”在不完全信息有限重复博弈中也成立,只要博弈重复的次数足够长,参与人有足够的耐心,任何满足个人理性的可行支付向量,都可以作为精炼贝叶斯均衡结果出现,不论p多么小。








没看懂,能不能说的明确一点啊