隐马尔可夫模型
出自 MBA智库百科(https://wiki.mbalib.com/)
隐马尔可夫模型(Hidden Markov Model,简称HMM)
目录 |
隐马尔可夫模型是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。
在正常的马尔可夫模型中,状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中,状态并不是直接可见的,但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。
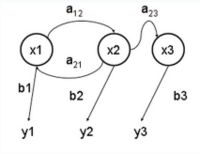
图:隐马尔可夫模型状态变迁图(例子)
x — 隐含状态
y — 可观察的输出
a — 转换概率(transition probabilities)
b — 输出概率(output probabilities)]]
“隐马尔可夫模型”最初是在二十世纪六十年代后半期Leonard E.Baum和其它一些作者在一系列的统计学论文中描述的。HMM最初的应用之一是开始于二十世纪七十年代中期的语音识别。
在二十世纪八十年代后半期,HMM开始应用到生物序列尤其是DNA的分析中。从那时开始,在生物信息学领域它们已经变得无处不在。
HMM有三个经典(canonical)问题:
- 已知模型参数,计算某一特定输出序列的概率.通常使用forward算法解决.
- 已知模型参数,寻找最可能的能产生某一特定输出序列的隐含状态的序列.通常使用Viterbi算法解决.
- 已知输出序列,寻找最可能的状态转移以及输出概率.通常使用Baum-Welch算法以及Reversed Viterbi算法解决.
另外,最近的一些方法使用Junction tree算法来解决这三个问题。
- 语音识别或光学字符识别
- 机器翻译
- 生物信息学和基因组学
- 基因组序列中蛋白质编码区域的预测
- 对于相互关联的DNA或蛋白质族的建模
- 从基本结构中预测第二结构元素
具体实例
假设你有一个住得很远的朋友,他每天跟你打电话告诉你他那天作了什么.你的朋友仅仅对三种活动感兴趣:公园散步,购物以及清理房间.他选择做什么事情只凭天气.你对于他所住的地方的天气情况并不了解,但是你知道总的趋势.在他告诉你每天所做的事情基础上,你想要猜测他所在地的天气情况.
你认为天气的运行就像一个马尔可夫链. 其有两个状态 "雨"和"晴",但是你无法直接观察它们,也就是说,它们对于你是隐藏的.每天,你的朋友有一定的概率进行下列活动:"散步", "购物", 或 "清理". 因为你朋友告诉你他的活动,所以这些活动就是你的观察数据.这整个系统就是一个隐马尔可夫模型HMM.
你知道这个地区的总的天气趋势,并且平时知道你朋友会做的事情.也就是说这个隐马尔可夫模型的参数是已知的.你可以用程序语言(Python)写下来:
states = ('Rainy', 'Sunny')
observations = ('walk', 'shop', 'clean')
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
transition_probability = {
'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
}
emission_probability = {
'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}
在这些代码中,start_probability代表了你对于你朋友第一次给你打电话时的天气情况的不确定性(你知道的只是那个地方平均起来下雨多些).在这里,这个特定的概率分布并非平衡的,平衡概率应该接近(在给定变迁概率的情况下){'Rainy': 0.571, 'Sunny': 0.429}<
transition_probability 表示基于马尔可夫链模型的天气变迁,在这个例子中,如果今天下雨,那么明天天晴的概率只有30%.代码emission_probability 表示了你朋友每天作某件事的概率.如果下雨,有 50% 的概率他在清理房间;如果天晴,则有60%的概率他在外头散步.








很棒的描述,謝謝