货币乘数论
出自 MBA智库百科(https://wiki.mbalib.com/)
货币乘数论(Money Multiplier Theory)
目录 |
乘数(亦称倍数)这个概念最早是由英国经济学家卡恩在1931年提出的。凯恩斯发挥了乘数原理,在1936年《通论》中提出了著名投资乘数论,成为有效需求原理的重要组成部分,此后新古典综合派又把乘数理论引伸到货币金融领域,提出了货币乘数论。
所谓货币乘数就是指基础货币扩张或收缩的倍数。他们认为,在狭义的货币定义下(即M1,现金加活期存款),货币供应量的决定因素有两个:一个是基础货币(用B表示),又称高能货币或强力货币,由现金与银行存款准备金组成,它是货币供应量(用Ms表示)变动的基础;另一个就是货币乘数(用m表示),这样货币供应量的基本公式可以表示为:Ms=Bm
货币乘数论的模型[1]
货币乘数论的模型大体可以分成简单乘数模型和复杂乘数模型两类。
1、简单乘数模型
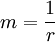
式中:
- m为货币乘数
- r为法定存款准备金率
假定商行经营中不保留超额准备金;基础货币也不以任何形式漏出存款领域。这个简单模型的结论,与凯恩斯的外生货币供应论是吻合的。
简单乘数模型以商业银行创造存款货币的过程为根据而提出的。在早期的论述中,新古典综合派进行的是简单的抽象分析,认为在现代银行制度下,商业银行能够通过其业务活动创造出存款货币来。这个过程简单地说就是:第一家商业银行在接受基础货币作为初始存款后,除了保留的法定准备金以外,均用于贷款或投资。第二家商业银行接受了由这笔贷款或投资转化而来的存款以后也是照此办理,通过各级商业银行延续的连锁反应,最终创造出数倍于该笔初始存款的存款货币。这个初始存款的派生倍数称为货币乘数,其数值等于法定存款准备金率的倒数。
2、复杂乘数模型
在简单乘数模型中有两个假定,即假定商业银行不保留超额准备金和假定原始存款不漏出存款领域。而在现实生活中,这两个假定是不切实际的。也就是说,实际上商业银行一般都因各种原因而保留一定的超额准备金,原始存款也在不断地漏出存款领域。这两部分金额如同法定存款准备金一样因退出了存款货币的派生过程,也影响着存款货币的扩张效果,因此,新古典综合派的萨缪尔森又把这两种因素考虑在内,在简单货币乘数模型的基础上提出了较为符合实际的复杂货币乘数公式。
萨缪尔森用“超额准备金率”来衡量商业银行超额准备的大小,用“现金漏损率”来衡量原始存款漏出存款领域的多少。超额准备金率是商业银行保留的超过法定准备金的准备金与存款货币的比率;现金漏损率是顾客在整个存款派生过程中所提取的现金总额与存款货币的比率。 如果用e表示超额准备金率,用c表示现金漏损率,货币乘数公式则变为:
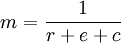
3、货币乘数论的基础:M1、M2。
货币乘数的理论模型[2]
我国现行的统计口径将货币供应量划分为M0、M1、M2和M3三个层次,其中M0是流通中的现金(M0),M = M0+活期存款(D),M2 = M1+全部定期存款(TD),M3 = M2+金融债券+商业票据+大额可转让定期存款+同业存款。其中,M1称为狭义的货币供应量,M2称为广义的货币供应量。
设B为基础货币,则B=C+存款准备金(TR);m为货币乘数,m1为M1相对于B的货币乘数,m2为M2相对于B的货币乘数,则货币供应量就由下式决定:
M1 = m1B = m1(C + TR) (1)
M2 = m2B = m2(C + TR) (2)
于是货币乘数M1、M2为:
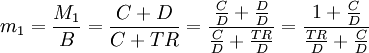 (3)
(3)
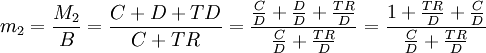 (4)
(4)
则有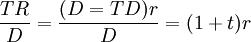
将k、t、r和TR/D代入(1)(2)式,化简,则得到乘数数m1和m2。
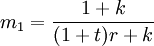 (5)
(5)
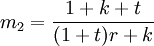 (6)
(6)
m1和m2都是k、r、t的函数,故(3)(4)式又可以写成
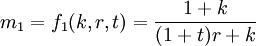 (7)
(7)
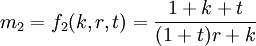 (8)
(8)
从上式可以看出,货币乘数是由通货-存款比率k、定期存款比率t和准备金比率r决定的。
评论(共11条)
上述m应该是存款乘数吧,货币乘数应该是 (1+c)/(r+e+c)
附上参考文献,您可以对比一下。谢谢您的参与!
台灣存款準備率在定存.活存都不同(rc=活存準備率.rd定存準備率.t=定存/活存) 所以貨幣乘數應該是 (1+c+t)/(c+rc+t*rd+e)
上述為廣義貨幣乘數; 狹義貨幣乘數(1+c)/(c+rc+t*rd+e) 補充 c=通貨/活存;e=超額準備/活存
增加了新的内容,希望对您有帮助~
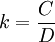 ,
,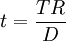 ,
,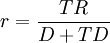 ,
,








不错