西北角法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　西北角法是从西北角（左上角）格开始，在格内的右下角标上允许取得的最大数；然后按行（列）标下一格的数；若某行（列）的产量（销量）已满足，则把该行（列）的其他格划去；如此进行下去，直至得到一个基本可行解的方法^[1]。

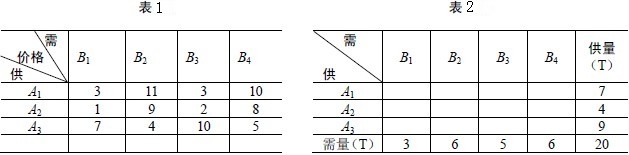
　　从表1中可知，总的产量=总的销量，故产销是平衡的。

　　第一步：列出运价表和调运物资平衡表。

　　运用表上作业法时，首先要列出被调运物资的运价表和供需平衡表（简称平衡表），如表1，2所示。

　　第二步：编制初始调运方案。

　　首先在表2的西北角方格（即左上角方格，对应变量x₁₁），尽可能取最大值：

　　x₁₁=min{3,7}=3

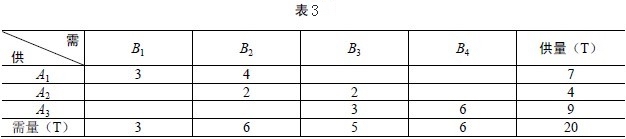
　　将数值3填入该方格(见表3)。由此可见x₂₁,x₃₁必须为0，即第一列其他各方格都不能取非零值，划去第一列。在剩下的方格中，找出其西北角方格x₁₂，

　　x₁₂=min{6,7-3}=4

　　将4填入它所对应方格，第一行饱和，划去该行。再找西北角方格x₂₂，

　　x₂₂=min{6-4,4}=2

　　将2填入x₂₂所对应方格，于是第二列饱和，划去该列。继续寻找西北方格为x₂₃，

　　x₂₃=min{5,4-2}=2

　　将2填入x₂3所对应方格，第二行饱和，划去该行。剩下方格的西北角方格为x₃3，

　　x₃3=min{5-2,9}=3

　　将3填入x₃₃所对应方格，第三列饱和，划去该列。最后剩下x₃₄方格，取x₃₄ = 6。

　　这样我们就找到了m＋n-1＝3＋5-1＝7个基变量，它们为：x₁₁ = 3,x₁₂ = 4,x₂₂ = 2,x₂₃ = 2,x₃₃ = 3,x₃₄ = 6。显然它们用折线连接后不形成闭回路。这就是西北角法所找初始基可行解，所对应的目标值为：

　　2×200＋1×250＋3×150＋1×150＋3×250＋3×300＋4×200＝4000

　　我们找到的初始基可行解可通过各行方格中数值之和是否等于产量，各列方格中数值之和是否等于销量来简单验证。

　　利用西北角法找初始基可行解简单可行，但也存在问题。例如在表3中可见c₃₅ = 4，单价高于该行其他各方格，最简单想法是单价小的情况下多运些货物，这样总运费会更小些，最小元素法就改进了西北角法的缺点。