保险纯费率
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
所谓保险纯费率,是指纯保费占保险金额的比率,是作为保险金用于补偿被保险人因保险事故造成保险标的的损失金额。
纯费率的确定[1]
依照费率厘定的原则,保险纯费率应当与保险事故发生的概率和保险事故发生后的赔偿金额有关。因此,确定纯费率,一方面要研究有效索赔的概率分布,也就是未来保额损失的可能性,即保额损失概率;另一方面要研究有效索赔的金额。我们通常按照统计学的原理,利用过去的数据来推断这两方面的指标,并由此得出有效索赔额的均值。通常采用的方法是,根据历年的有效索赔数额,计算出单位保额的平均有效索赔额,即平均保额损失率。然后,用其近似的估计未来单位保额的有效索赔额,进而确定纯费率。
纯费率的计算[1]
其计算公式为:纯保费=保额损失率±均方差
1.确定保额损失率
保额损失率是赔偿金额占保险金额的比率。其计算公式为:
|
保额损失率= | 赔偿金额 |
X 100% |
| 保险金额 |
由于保险事故的发生在实践上具有很强的随机性,只有在一个较长的时期里才比较稳定,因此纯费率的计算应当取一个较长时期的数据,通常不少于5年。若知各年的保额损失率,则可计算平均保额损失率。平均保额损失率的计算公式为:
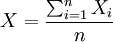
2.计算均方差
均方差是各保额损失率与平均损失率离差平方和平均数的平方根。它反映了各保额损失率与平均保额损失率相差的程度,说明了平均保额损失率的代表性,均方差越小,则其代表性越强;反之,则代表性差。若以S表示均方差,则其计算公式为:
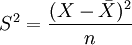
对于平均保额损失率附加均方差的多少,取决于损失率的稳定程度。对于损失率较稳定的,则其概率 不要求太高,相应地概率度 为1即可;反之,则要求概率较高,以便对高风险的险种有较大的把握,从而稳定经营,相应的概率度为2或3。
3.计算稳定系数
稳定系数是均方差与平均保额损失率之比。它衡量期望值与实际结果的密切程度,即平均保额损失率对各实际保额损失率的代表程度。稳定系数越小,保险经营稳定性越高;反之,稳定系数越大,保险经营的稳定性越低。一般认为,稳定系数在10%~20%是较为合适的。稳定系数的计算公式为:
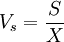
4.确定纯费率
其计算公式为:
纯保费=保额损失率±均方差=保额损失率×(1±稳定系数)
实例[1]
例如:某保险公司某类保险业务过去5年期间每年的保额损失率分别为0.30%,0.25%,0.26%,0.24%,0.20%,求来年的纯费率。
解:首先,计算以往5年平均保额损失率,为:
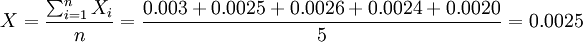
其次,计算均方差。为了方便计算,如下表所示:
| 年份 | 保险损失率(X) | 离差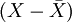 | 离差的平方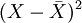
|
| 1 | 0.30% | 0.05% | 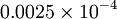
|
| 2 | 0.25% | 0 | 0 |
| 3 | 0.26% | 0.01% | 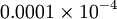
|
| 4 | 0.24% | -0.01% | 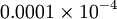
|
| 5 | 0.20% | -0.05% | 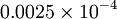
|
| n=5 | 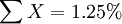 |  | 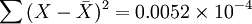
|
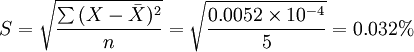
然后,计算稳定系数。
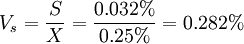
最后,根据前面的叙述,本例的保险业务经营比较稳定,可考虑在同种业务的纯费率中加1个均方差,因此:
纯费率=0.25%+0.032%=0.282%







