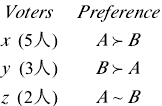策略投票
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
策略投票是指投票人通过在投票中谎报自己的真实偏好,使投票结果发生有利于自己的变化。人们很早就注意到这种‘策略行为’在投票选举中的存在。投票选举理论的奠基人Dodgson经过大量对比研究认为:投票程序的可操纵性和投票人策略投票的行为是普遍存在的。在Arrow不可能定理的基础上,Gibbard(1973)和Satterthwaite(1975)提出了Gibbard--Satterthwaite防策略投票不可能定理,从理论上证明策略投票的必然性。之后的很多研究者对防策略投票问题进行了研究。
投票人的策略投票行为与投票规则有关,在某些投票规则(如PR)下策略投票很少发生,在另一些投票规则(如BR)下策略投票发生的可能性较大。在本节中我们将分析策略投票的原因,并探讨防止策略投票的方法。
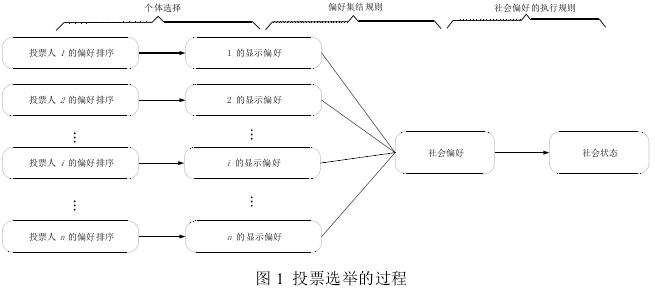
投票选举的过程可以表示为图1的形式。在个体选择阶段投票人以选票方式将自己的偏好表示出来,偏好集结过程将所有个体偏好集结为社会偏好,然后根据社会偏好确定一种予以执行的方案(或社会状态)。投票人在个体选择阶段是真实投票还是策略投票取决于整个投票过程的规则。
根据对投票过程的划分,投票规则可以分为三个部分:产生备选方案的规则,个体偏好集结函数,对社会偏好的执行规则。其中对社会偏好的执行规则是指如何根据社会偏好选择一个得以执行的方案,它往往与个体偏好集结函数结合在一起。最普遍的对社会偏好的执行规则是所谓的‘胜者全得’,即在社会偏好排序中排在第一位的候选方案将成为唯一得到执行的方案。例如Condorcet规则的集结函数是对备选方案两两比较,如果某一备选方案在两两比较中优于其它任何方案,它就成为获胜者,同时它也成为将被执行的方案。与此相反,PR的社会偏好的执行规则是根据社会偏好按比例地分配选举收益。
接下来我们就来分析三个导致策略投票的原因。
1.产生备选方案的规则导致策略投票行为。
怎样产生备选方案的问题以及它和策略投票行为的关系在以往的研究中常被忽视,但不公平的备选方案确实会导致策略投票行为。
例4:一个委员会有10名成员,他们将用SMV规则对一块空地的使用进行投票表决,目的是选择唯一的使用方案。现在假定以某种独裁方式提出了两个备选方案。方案A:在空地上建足球场;方案B:在空地上建游泳池。委员会中的5名成员支持方案A,3名成员支持方案B,另外2名成员既不支持A也不支持Bo
如果所有成员都真实投票,社会偏好应该是AFB。但如果成员们的偏好是公开的,那么投票结果将很可能是A一B,使两种方案被推迟。容易验证在已有的任何一种投票规则下投票人z都有策略投票的激励。导致这样结果的原因是产生备选方案的规则不公平。例如,投票人z可能最希望在空地上建网球场,但这种偏好无法通过投票显示出来,因此z可能通过策略投票行为减少自己的损失。
2.偏好集结函数的缺陷导致策略投票行为。
偏好集结函数的缺陷(如SMV或Condorcet规则导致的多数票循环,BR对弱序的处理等)是导致策略投票行为的另一个原因。
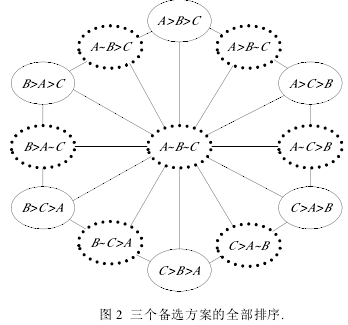
下面以三个备选方案的投票为例说明偏好集结函数怎样影响个人投票行为。在三个备选方案的情况下,投票人对方案的排序总共有13种可能,我们把这些可能的排序表示为图2。图2既是投票人偏好的集合,也是作为个体偏好集结结果的社会偏好的集合。在发生偏好强度悖论的情况下,社会偏好将不满足传递性,偏好集结的结果将超出图2的排序范围。在这种情况下,一方面投票人真实投票的结果变得不可预测,另一方面具有某些特定偏好排序的投票人可能处于独裁或寡头的位置。
3.3对社会偏好的执行规则导致策略投票行为。
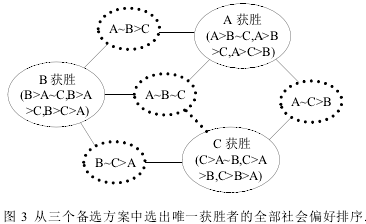
最普遍的对社会偏好的执行规则是选择唯一的获胜者,获胜的候选人(或备选方案)独占全部选举收益。这种‘胜者全得’的投票规则是对社会偏好的一种扭曲,它使社会偏好中除获胜者以外的备选方案的排序变得没有意义。例如,在对三个备选方案A,B和C的投票选举中,如果最后A胜出,则实际社会偏好是A>B>C或是A>C>B或A>B>C变得没有差别。我们用图3表示从三个备选方案中选出唯一获胜者的社会偏好集合。与图1相比它的可能社会状态缩小为7种。假设对于全部备选方案之中的B和C每个投票人都认为B>C,这样社会偏好中也应该有B>C。但如果最后始终是A胜出,那么社会偏好中B>C的排序变得没有意义,投票人也就失去了把B排在C前面的激励。这是导致策略投票的又一原因。
比例代表制(PR)是一种避免偏好强度悖论的投票规则,并且它对社会偏好的执行规则不是‘胜者全得’,在备选方案适当的情况下它将是防策略投票的。
在第二节中我们已经讨论了备选方案之间相关性的问题,如何选择备选方案不仅关系到选举的公平性也对策略投票行为的发生有重要影响。对于例4中两个备选方案的投票问题,即使采用PR规则,具有A一B偏好的投票人仍然可能寻求策略投票,因为他所期望的方案并不在备选方案之中。
以下的定理表明:如果每个投票人最喜好的方案都在备选方案集合中,采用PR规则可以避免策略投票行为。
定理1:如果对备选方案不加限制,一人一票的比例代表制是防策略投票的。i1F眼如果一个投票规则使每个投票人在真实投票的情况下取得最大收益,这样投票人就没有采用策略投票的激励,这种投票规则必然是防策略投票的。因此,只需要证明PR规则下任何投票人在真实投票的情况下取得最大收益。
对于n个投票人、采用PR规则的投票选举,设选举总收益为U。首先我们将证明任何投票人至少可以取得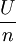 的收益。既然对备选方案没有限制,任意一个投票人i(i∈n)总可以提出一个方案,并使该方案获得至少一票。因此,只要i提出一个对自己完全有利的备选方案并投票给此方案,就至少可以分配到
的收益。既然对备选方案没有限制,任意一个投票人i(i∈n)总可以提出一个方案,并使该方案获得至少一票。因此,只要i提出一个对自己完全有利的备选方案并投票给此方案,就至少可以分配到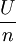 的收益。
的收益。
接下来我们将证明投票人i只能从他投票支持的备选方案中取得收益。设i最喜好的备选方案是j(这以为着i从方案j中至少获得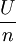 的收益)。假设i投票给备选方案j,而且从备选方案k获得收益
的收益)。假设i投票给备选方案j,而且从备选方案k获得收益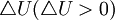 。这时i获得的选举收益至少为
。这时i获得的选举收益至少为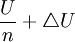 。在这种情况下至少有一个投票人的收益少于旦,这表明假设错误,因此投票人只能从他投票支持的备选方案中取得收益。
。在这种情况下至少有一个投票人的收益少于旦,这表明假设错误,因此投票人只能从他投票支持的备选方案中取得收益。
由于任何投票人只可能从他投票支持的方案中获利,因此每个人都将选择他最喜好的备选方案,这时选举结果中每个投票人的收益都是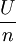 。如果某个投票人没有真实投票,他的收益不可能超过
。如果某个投票人没有真实投票,他的收益不可能超过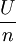 ,因此不存在策略投票的激励。
,因此不存在策略投票的激励。
定理1表明存在一种防策略投票的投票规则,并且从定理的证明过程中可知在这种投票规则下选举收益在投票人中平均地分配。这提醒我们在这样的规则下投票选举可以得到公平的结果。