回归直线法
出自 MBA智库百科(https://wiki.mbalib.com/)
回归直线法(Linear Regression Method)
目录 |
根据若干期业务量和成本的历史资料,运用最小平方法原理计算固定成本(或混合成本中的固定成本)和单位变动成本(或混合成本中变动部分的单位额)的一种成本性态分析方法。
回归直线法的由来[1]
回归直线法也称直线回归法,“回归”名称的由来归功于英国统计学家高顿F·Glton(1822-1911)和他的学生皮尔森K·Pearson(1857-1936),他们在研究父母身高与其子女的遗传问题时,发现高个子父辈的儿子们的平均高度要低于他们父辈的平均高度,矮个子父辈的儿子们的平均身高要高于他们父辈的平均身高,也就是说,没有出现父辈个子高其儿子更高,父辈个子矮其儿子更矮的两极分化现象,而都是朝标准身高(69.69inch)靠近)为了描述这种有趣的现象,高顿引进了“回归”这个名词来描述父辈身高x与子代身高y的这种直线关系:
y=33.73+0.516x
说明子代的身高朝着标准身高“回归”,为了纪念高顿这个伟大的统计学家,以后被引申到把研究一个或一组非随机变量来估计或预测某一个随机变量的观察值时,所建立的数学模型及所进行的统计分析,统称为“回归”分析。
如以业务量为自变量,成本为因变量,它们之间具有线性关系,则它们之间的关系可用下式表示:
y=a+bx
式中y代表总成本,a代表固定成本,b代表单位变动成本,x代表业务量。利用这个方程,就可认识和掌握成本在一定条件下的增减变动趋势,公式为:
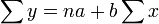
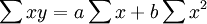
a,b的公式为:
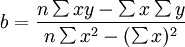
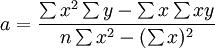
另外,求出b后,a还可以这样求解
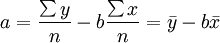
回归直线的相关性检验[1]
根据回归直线法,无论任何一组历史数据资料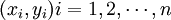 ,都可利用最小二乘法求得回归直线
,都可利用最小二乘法求得回归直线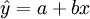 而不需要事先假定y与x具有线性相关关系,也就是说,虽然所求直线
而不需要事先假定y与x具有线性相关关系,也就是说,虽然所求直线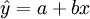 与其他所有直线相比,各点纵坐标
与其他所有直线相比,各点纵坐标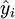 与历史数据y_i之误差平方和最小,但并不等于能很好地拟合历史数据所确定的各个点(即x与y不一定相关),有时这种拟和甚至毫无意义,因此,必须进行相关性检验,所谓“相关性检验”,就是验证所有的历史数据
与历史数据y_i之误差平方和最小,但并不等于能很好地拟合历史数据所确定的各个点(即x与y不一定相关),有时这种拟和甚至毫无意义,因此,必须进行相关性检验,所谓“相关性检验”,就是验证所有的历史数据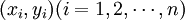 是否大致在一条直线上。
是否大致在一条直线上。
所采用的方法,有方差分析法和相关系数法,根据统计学原理,在概率为正态分布的情况下,随机变量出现在期望值±1个标准差范围内的概率有68.26%,出现在期望值±2个标准差范围内的概率有95.44%,出现在期望值±3个标准差范围内的概率有99.72%(期望值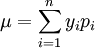 ,其中:p_i为第i个随机变量的概率,标准差
,其中:p_i为第i个随机变量的概率,标准差 )因此,随机变量出现在期望值±3个标准差之外的概率为0.28%=0.0028,而单侧概率只有0.14%=0.0014,我们不妨认为,实际值与期望值的最大误差不超过±3个标准差,即实际值一般都在区间[μ − 3σ,μ + 3σ]上,为便于查表,取随机变量出现在期望值±3个标准差之外的概率α = 0.005(α称为显著性水平或检验水平)。在此基础上,介绍相关系数法和方差分析法。
)因此,随机变量出现在期望值±3个标准差之外的概率为0.28%=0.0028,而单侧概率只有0.14%=0.0014,我们不妨认为,实际值与期望值的最大误差不超过±3个标准差,即实际值一般都在区间[μ − 3σ,μ + 3σ]上,为便于查表,取随机变量出现在期望值±3个标准差之外的概率α = 0.005(α称为显著性水平或检验水平)。在此基础上,介绍相关系数法和方差分析法。
- 1.相关系数法
相关系数法就是计算相关系数![r=\frac{n\sum^n_{i=1}x_i y_i-\sum^n_{i=1}x_i\sum^n_{i=1}y_i}{\sqrt{\left[n\sum^n_{i=1}x^2_i-(\sum^n_{i=1}x_i)^2\right]\left[n\sum^n_{i=1}y^2_i-(\sum^n_{i=1}y_i)^2\right]}}](/w/images/math/9/4/b/94bcad614b38e7d5747d61023759d3ac.png)
然后利用相关系数临界值表查出r(α,n),若r > r(α,n),说明x与y存在线性关系,从而可建立直线方程y=a+bx,否则,说明x与y不存在线性关系,建立直线方程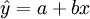 毫无意义。
毫无意义。
- 2.方差分析法
设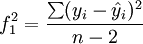
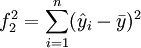
方差分析法就是计算
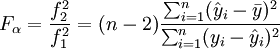
然后利用F分布表查出Fα(1,n − 2)值,若Fα > Fα(1,n − 2),说明x与y存在线性关系,从而可建立直线方程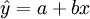 。
。
回归直线的误差估计[1]
误差估计的方法很多,简单的误差估计有以下3种:
- 1.最大误差法
最大误差法是用历史数据各期实际值与预测值误差绝对值除以该期对应的自变量,取其最值,乘以预测期自变量,作为最大误差的一种方法。
最大误差=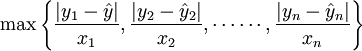
- 2.平均误差法
平均误差法是用距预测期最近的n期历史数据中,每期实际值与预测值误差的绝对值除以该期自变量,求和后乘 ,再乘预测期的自变量,作为估计误差的一种方法。
,再乘预测期的自变量,作为估计误差的一种方法。
- 3.标准差法
标准差法是用标准差与置信概率的关系来进行误差估计的一种方法。
标准差=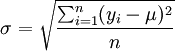
总之,回归直线法的实质是以直线代替曲线,因此,不论在成本性态分析,还是在销售预测、成本预测、利润预测、资金预测以及其它方面,都必须进行相关性检验和误差估计,否则,其结果就不可靠。
借助于回归直线法,可以使半变动成本的分解建立在科学分析和精确计算的基础上。但计算工作量较大,比较麻烦。如能使用电子计算机计算,这种方法将会得到广泛应用。







