对称循环应力
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
对称循环应力(Symmetry Circulating Stress)
目录 |
[编辑]
什么是对称循环应力[1]

[编辑]
对称循环应力下构件的疲劳强度条件[2]
![[\sigma_{-1}]=\frac{(\sigma_{-1})}{n_f}=\frac{\epsilon_\sigma \beta}{n_fK_\sigma}\sigma_{-1}](/w/images/math/5/d/1/5d151a30cb8aab95091e6703adbd57c9.png) (1)
(1)![\sigma_{max}\le [\sigma_{-1}]=\frac{\epsilon_\sigma \beta}{n_fK_\sigma}\sigma_{-1}](/w/images/math/0/3/0/0302fccdb28b7f6306d20d095016539b.png) (2)
(2)式中σmax代表拉压杆与梁横截面上最大的工作应力。
工程上大都采用安全因数法建立构件的疲劳强度条件,即要求构件的实际安全因数不小于规定的安全因数。由(1)、(2)两式可知,拉压杆与梁在对称循环应力下的工作安全因数为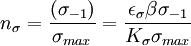 (3)
(3)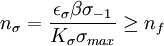 (4)
(4)![\tau_{max}\le [\tau_{-1}]=\frac{\epsilon_\tau \beta}{n_fK_\tau}\tau_{-1}](/w/images/math/c/6/6/c6699c869698888d317e65d443e5b814.png) (5)
(5)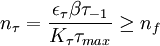 (6)
(6)式中,τmax代表横截面上的最大切应力。
[编辑]
[编辑]







