加权几何平均数
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
(重定向自加权几何平均法)
加权几何平均数（weighted geometric mean）
目录 |
[编辑]
加权几何平均数是在变量值次数(或比重)不相等时，用加权的方法计算出的几何平均数。几何平均数是n个正标志值的连乘积的n次方根。当标志值出现的次数相同时，用简单几何平均数的公式计算；当标志值出现的次数不同时，用加权几何平均数的公式计算。几何平均数的应用特点是： 受极端标志值的影响，但较算术平均数和调和平均数为小： 计算几何平均数的各项标志值必须是大于0的正数；应用范围较窄，它是计算平均比率或平均发展速度较适合的一 种方法
根据统计资料的不同，几何平均数也有简单几何平均数和加权几何平均数之分。
加权几何平均数，是统计学中的一种动态平均指标，多是指社会经济现象的同质总体在时间上变动速度的平均数。加权几何平均数是各标志值fi次方的连乘积的次方根。
当各个变量值的次数(权数)不相同时，应采用加权几何平均数 。
[编辑]
![G=\sqrt[\sum f]{X_1^{f_1}\times X_2^{f_2}\times\ldots\times X_n^{f_n}}=\sqrt[\sum^n_{i=1}f]{\prod_{i=1}^N X_i^{f_i}}](/w/images/math/d/e/c/dec3cab26e5223b43a310cac18127ea1.png)
式中，fi为变量值Xi出现的次数，又称权数。
[编辑]
例如，投资银行某笔投资的年利率是按复利计算的，10年的年利率分配是：第1年至第2年为5%；第3年至第5年为8%；第6年至第8年为10%；第9年至第10年为12%，则：
平均年利率＝平均本利率-1
![=\sqrt[10]{1.05^2\times1.08^3\times1.1^3\times1.12^2}-1](/w/images/math/e/8/0/e80fe1cf3422703856b2805527c08c08.png)
=108.7743%-1
=8.7743%
问题：如果不按复利计算，平均年利率是多少？
解：设本金为C，则：
平均年利率=平均利息/本金
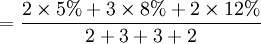
=8.8%
[编辑]
以上第一步计算少加了3×C×10%