克莱因瓶

出自 MBA智库百科(https://wiki.mbalib.com/)

克莱因瓶（Klein bottle）

　　在数学领域中，克莱因瓶（Klein bottle）是指一种无定向性的平面，比如二维平面，就没有“内部”和“外部”之分。在拓扑学中，克莱因瓶（Klein Bottle）是一个不可定向的拓扑空间。克莱因瓶最初由德国几何学大家菲立克斯·克莱因 (Felix Klein) 提出。在1882年，著名数学家菲立克斯·克莱因 (Felix Klein) 发现了后来以他的名字命名的著名“瓶子”。克莱因瓶的结构可表述为：一个瓶子底部有一个洞，现在延长瓶子的颈部，并且扭曲地进入瓶子内部，然后和底部的洞相连接。和我们平时用来喝水的杯子不一样，这个物体没有“边”，它的表面不会终结。它和球面不同 ，一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面，即它没有内外之分。

　　“克莱因瓶”这个名字的翻译其实是有些错误的，因为最初用德语命名时候名字中“Kleinsche Fläche”是“克莱因平面”的意思。因为翻译问题写成了Flasche，这个词才是瓶子的意思。不过不要紧，“瓶子”这个词用起来也非常合适。

　　在1882年，著名数学家菲利克斯·克莱因（Felix Klein）发现了后来以他的名字命名的著名“瓶子”。这是一个像球面那样封闭的（也就是说没有边）曲面，但是它却只有一个面。在图片上我们看到，克莱因瓶的确就像是一个瓶子。但是它没有瓶底，它的瓶颈被拉长，然后似乎是穿过了瓶壁，最后瓶颈和瓶底圈连在了一起。如果瓶颈不穿过瓶壁而从另一边和瓶底圈相连的话，我们就会得到一个轮胎面（即环面）。

　　克莱因瓶是一个不可定向的二维紧流形，而球面或轮胎面是可定向的二维紧流形。如果观察克莱因瓶，有一点似乎令人困惑－－克莱因瓶的瓶颈和瓶身是相交的，换句话说，瓶颈上的某些点和瓶壁上的某些点占据了三维空间中的同一个位置。

　　我们可以把克莱因瓶放在四维空间中理解：克莱因瓶是一个在四维空间中才可能真正表现出来的曲面。如果我们一定要把它表现在我们生活的三维空间中，我们只好将就点，把它表现得似乎是自己和自己相交一样。克莱因瓶的瓶颈是穿过了第四维空间再和瓶底圈连起来的，并不穿过瓶壁。用扭结来打比方，如果把它看作平面上的曲线的话，那么它似乎自身相交，再一看似乎又断成了三截。但其实很容易明白，这个图形其实是三维空间中的曲线。它并不和自己相交，而是连续不断的一条曲线。在平面上一条曲线自然做不到这样，但是如果有第三维的话，它就可以穿过第三维来避开和自己相交。只是因为我们要把它画在二维平面上时，只好将就一点，把它画成相交或者断裂了的样子。克莱因瓶也一样，我们可以把它理解成处于四维空间中的曲面。在我们这个三维空间中，即使是最高明的能工巧匠，也不得不把它做成自身相交的模样；就好像最高明的画家，在纸上画扭结的时候也不得不把它们画成自身相交的模样。有趣的是，如果把克莱因瓶沿着它的对称线切下去，竟会得到两个莫比乌斯环。

　　如果莫比乌斯带能够完美的展现一个“二维空间中一维可无限扩展之空间模型”的话，克莱因瓶只能作为展现一个“三维空间中二维可无限扩展之空间模型”的参考。因为在制作莫比乌斯带的过程中，我们要对纸带进行180°翻转再首尾相连，这就是一个三维空间下的操作。理想的“三维空间中二维可无限扩展之空间模型”应该是在二维面中，朝任意方向前进都可以回到原点的模型，而克莱因瓶虽然在二维面上可以向任意方向无限前进。但是只有在两个特定的方向上才会回到原点，并且只有在其中一个方向上，回到原点之前会经过一个“逆向原点”，真正理想的“三维空间中二维可无限扩展之空间模型”也应该是在二维面上朝任何方向前进，都会先经过一次“逆向原点”，再回到原点。而制作这个模型，则需要在四维空间上对三维模型进行扭曲。数学中有一个重要分支叫“拓扑学”，主要是研究几何图形连续改变形状时的一些特征和规律的，克莱因瓶和莫比乌斯带变成了拓扑学中最有趣的问题之一。莫比乌斯带的概念被广泛地应用到了建筑，艺术，工业生产中。

　　克莱因瓶定义为正方形区域 [0,1]×[0,1] 模掉等价关系(0,y)~(1,y), 0≤y≤1 和 (x,0)~(1-x,1), 0≤x≤1。类似于 Mobius Band, 克莱因瓶不可定向。但 Mobius 带可嵌入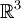，而克莱因瓶只能嵌入四维（或更高维）空间。

• 莫比乌斯带
• 彭罗斯楼梯