优先矩阵

出自 MBA智库百科(https://wiki.mbalib.com/)

优先矩阵(precedence matrix)

　　优先矩阵是针对通过头脑风暴得到的众多面临问题或解决问题的措施，确定优先解决的问题或优先采取的措施的方法。

　　优先矩阵具备3个优点：

　　·它是确定主要薄弱环节的一种有效手段，这些环节的运营可能已经严重阻碍或妨碍了主要改进目标的实现。

　　·它提供了确立优先顺序的可能，以便把资源分配到改进过程上来。

　　·它有助于团结一支管理队伍来支持各方一致同意的优先环节。

　　优先矩阵的目的是帮助人们在矩阵图或树图的分析中，根据权重系数和决定准则测量／评价关联性，以决定要优先实施的方案。

　　一旦我们通过诸如关系矩阵图、关联图、树图或其他方法构建／识别了关联和选项／可选方案后，一般就要进入决定阶段。优先矩阵可以让我们进行相关比较，并以一种有组织的方式表达信息，这样我们可以根据一致、客观和量化的评价支持我们做出的决定。

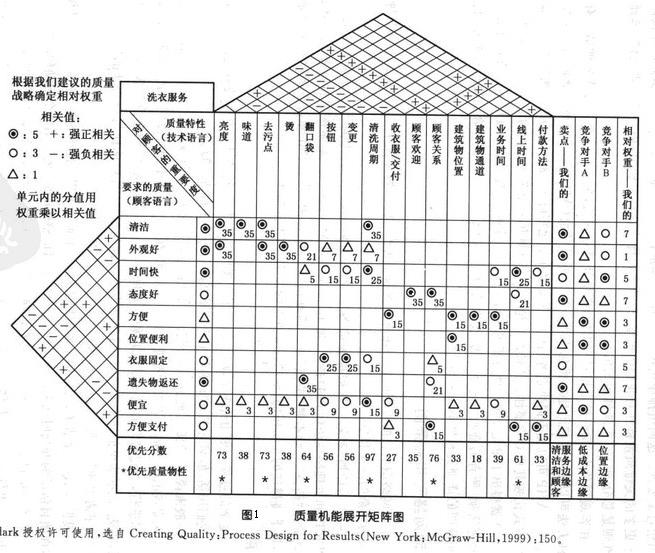
　　在主观的评估中，每个人根据过去的经验和对未来的理解，集体地使用某种同意／投票／基本排序的过程，这些方法包括排序／投票计划——德菲里(Delphli)方法、名义小组技术和其他方法。图1所示的矩阵图包括了两组排序，一个是主体部分的关联强度，一个是卖点的相对重要性。这两组排序让我们对矩阵主体进行量化并确定质量特性分值。因此我们用了更多的关键质量特性对我们的思维／行动进行优化。在本例中，用“*”代表关键，选择的准则是总分60分(主观确定的值)。

　　在客观评估中，我们指定相对权重值，定量计算这些值，集中到一个相对优先的数。有几种方法可以用于客观地建立优化准则。分析分层过程(AHP)是一种被广泛使用的量化技术。AHP可以让不同决定者的优先事项放在优化矩阵中，通过该矩阵和决定准则以成对的方式比较其相对重要性。比较结果包括决定准则优先矩阵和相应的可选择优先权重矩阵，这样就得出了量化小组一致分析的矩阵。从这个分析中，我们就可以用一定的置信水平选择可选项，所有的准则——经济的、技术的和无形的要素——都被整合到决定过程中。