混合策略納什均衡
出自 MBA智库百科(https://wiki.mbalib.com/)
混合策略納什均衡(Mixed Strategy Nash Equilibrium)
目錄 |
混合策略納什均衡:在n個參與人的博弈G={S1 ,... Sn ; u1 ,...un}中,混合策略組合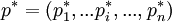 構成一個納什均衡,如果對於所有的i=1,2...,n下式成立:
構成一個納什均衡,如果對於所有的i=1,2...,n下式成立:
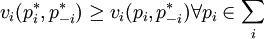
也就是說,如果一個策略組合使任何一個參與人的策略都是相對於其他參與人的策略的最佳策略,這個策略就構成一個納什均衡,不管這個策略是混合策略還是純策略。
混合策略納什均衡是面對其他博弈者選擇的不確定性的一個理性對策,其主要特征是作為混合策略一部分的每一個純策略有相同的期望值,否則,一個博弈者會選擇那個期望值最高的策略而排除所有其他策略,這意味著原初的狀態不是一個均衡。
1、最大化支付法:即最大化各個參與人的效用函數。
2、支付相等法:根據前面分析的猜硬幣博弈中參與人的策略的思路,每個參與人的混合策略都使其餘參與人的任何純策略的期望支付相等,因此,解混合策略納什均衡可以令參與人的各個純策略支付相等,構成方程組求解。
混合策略納什均衡的經典博弈——猜謎博弈[1]
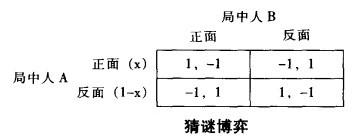
兩個局中人A、B手裡各拿一枚硬幣,每人可以選擇正面向上或反面向上,然後同時亮出,如果兩枚硬幣正反面相同,B付給A1元錢,如果兩枚硬幣正反面不相同,A付給B1元錢。在這種情況下,局中人A、B如何選擇呢?下圖給出這個博弈的雙變數收益矩陣。
這是一個兩人零和博弈,在每一個結局中一方所得即為另一方所失,即兩個局中人的收益之和恰好等於零。在雙變數收益矩陣中採用畫線的方法,在這個博弈中找不到純策略納什均衡。
那麼,猜謎博弈是否存在混合策略納什均衡呢?1950年納什證明瞭任何有限博弈都至少存在一個納什均衡(包括純策略納什均衡和混合策略納什均衡)。
猜謎博弈不存在純策略納什均衡,那麼根據納什的證明一定存在混合策略納什均衡。
混合策略納什均衡的求解方法
2×2雙量矩陣博弈局中人1,2的收益矩陣分別是
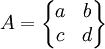
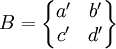
以X=(x,1-x),Y=(y,1-y)分別表示局中人1,2的混合策略,其中0≤x≤1,0≤y≤1
令
Q=a-b-C+d,q=d-b (2.1)
R=a'-b'-C'+d',r=d'-C’ (2.2)
則博弈的均衡點根據不同Q,q,R,r的值由下麵的(1)和(2)兩組不等式確定:
(1)當Q=o且q=o時,o≤x≤1,o≤y≤1 (2.3)
當Q=0,q>0時,x=o,o≤y≤1 (2.4)
當Q=0,q<o時,x=1,o≤y≤1 (2.5)
當Q>0時,
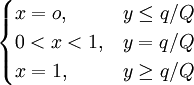 (2.6)
(2.6)
當Q<0時,
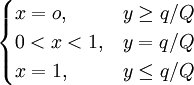 (2.7)
(2.7)
(2)當R=0且r=0時,0≤x≤1,0≤y≤1 (2.8)
當R=0且r>0時,0≤x≤1,y=0 (2.9)
當R=0且r<0時,0≤x≤1,y=1 (2.10)
當R>0時,
 (2.11)
(2.11)
當R<0時,
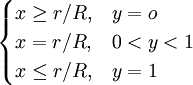 (2.12)
(2.12)
將不等式(2.3)至式(2.7)中滿足博弈條件的一組與式(2.8)至式(2.12)中滿足條件的一組聯立起來,即可求得與均衡點相對應的菇值和Y值。
下麵用雙變數矩陣博弈混合策略納什均衡的求解方法來尋找猜謎博弈的納什均衡。
設猜謎博弈局中人A與局中人B的收益矩陣分別是
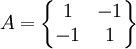
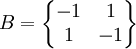
X=(x,1-x)表示局中人A的混合策略,其中0≤x≤1,x表示選擇正面。
Y=(y,1-y)表示局中人B的混合策略,其中0≤y≤1,Y表示選擇正面。
利用式(2.1)和式(2.2)計算Q,q,R,r:
Q=4>0, q=2
R=-4<0, r=-2
將這些數值代入式(2.6)和式(2.12),得到
 (2.13)
(2.13)
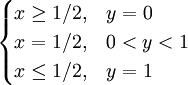 (2.14)
(2.14)
解這些不等式,求得博弈的納什均衡
(x,y)=(1/2,1/2) (2.15)
即局中人A與局中人B的混合策略
(x,Y)=((x,1-x),(y,1-y))
=((1/2,1/2),(1/2,1/2))(2.16)
式(2.16)表示局中人A以1/2的概率選擇正面,同時也以1/2的概率選擇反面;同樣局中人B也以1/2的概率選擇正面,以1/2的概率選擇反面。
這個混合策略納什均衡的實際背景是:如果猜謎博弈一遍又一遍地重覆很多次,兩個局中人每次獨立地等可能(即概率為1/2)從正面和反面兩個純策略中選擇一個作為此次的行動,那麼從平均意義上來說,兩個局中人的期望收益都為0,誰也不輸誰也不贏,均衡表現為一種握手言和的結局。
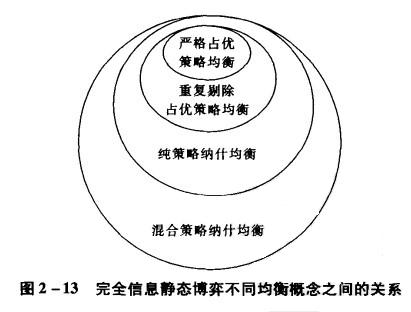
混合策略納什均衡博弈與其他均衡的關係[1]
嚴格占優策略均衡、重覆剔除的占優策略均衡、純策略納什均衡和混合策略納什均衡。一般將上述四種均衡統稱為納什均衡。
在這四種均衡概念中每種均衡依次是前一種均衡的擴展。前一種均衡是後一種均衡的特例。嚴格占優策略均衡是重覆剔除的占優策略均衡的特例;重覆剔除的占優策略均衡是純策略納什均衡的特例;純策略納什均衡是混合策略納什均衡的特例。
如果將完全信息靜態博弈中存在某種均衡的所有博弈定義為一個集合,那麼就存在前一種均衡的博弈集合是後一種均衡的博弈集合的子集。完全信息靜態博弈四種均衡概念之間的關係可以用圖2—13表示。






what's Q and q here?