分期付款
出自 MBA智库百科(https://wiki.mbalib.com/)
分期付款(Pay by Installments)
目錄 |
分期付款是購買商品和勞務的一種付款方式。大多用在一些生產周期長、成本費用高的產品交易上。如成套設備、大型交通工具、重型機械設備等產品的出口。
分期付款方式是在第二次世界大戰以後發展起來的。開始時只局限於一般日用商品或勞務的購買。後來,隨著生產力的迅速發展,工、農業生產的規模日益擴大,所需費用增大,加之銀行信用的發展,分期付款的領域擴大到企業購買大型機器設備和原材料上。
近年來伴隨著中國金融服務的完善以及人們消費習慣的改變,在國外流行的分期付款消費被引入國內,並迅速得到國內消費者的認可。採用分期付款方式消費的通常是目前支付能力較差,但有消費需求的年輕人。其消費的產品通常是筆記本電腦、手機、數位產品等。
分期付款的做法是在進出口合同簽訂後,進口人先交付一小部分貨款作為訂金給出口人,其餘大部分貨款在產品部分或全部生產完畢裝船付運後,或在貨到安裝、試車、投入以及質量保證期滿時分期償付。
分期付款實際上是賣方向買方提供的一種貸款,賣方是債權人,買方是債務人。買方在只支付一小部分貨款後就可以獲得所需的商品或勞務,但是因為以後的分期付款中包括有利息,所以用分期付款方式購買同一商品或勞務,所支付的金額要比一次性支付的貨款多一些。
買賣雙方在成交時簽訂契約,買方對所購買的商品和勞務在一定時期內分期向賣方交付貨款。每次交付貨款的日期和金額均事先在契約中寫明。
銀行為消費者提供相當於所購物品金額的個人消費貸款,消費者用貸款向供應商支付貨款,
一方面可以使賣方完成促銷活動;
另一方面也給買方提供了便利。
分期付款的計算方法 [1]
在分期付款中還要瞭解分期付款的有關計算。
- 1.等額償還方式
若年初向銀行貸款D(元),準備分n期償還,每期均償還P(元),期利率為R。
貸款一期後,本金和應為D(1+R)。
第一次還款後剩餘款項為b1 = D(1 + R) − P,由於所剩款項要付利息,故第二次還款是在(D(1+R)-P)(1+R)的基礎上還P元,即第二期償還後剩餘款項為:
b2 = D(1 + R)2 − P(1 + R) − P
故有:![b_n=D(1+R)^n-P[(1+R)^{n-1}+(1+R)^{n-2}+\cdots\cdots+1]=0](/w/images/math/7/0/0/700973cd33188674f4221d6cdaa4c0a4.png)
即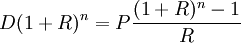
從而每期應償還的數目為
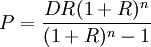
- 2.不等額償還
如果不是每期都償還P元,而是第一期還P1,第二期還P2, …第n期還Pn後,便立即結算。
則:第一期償還後,還剩:
D(1 + R)n − P1
第二期償還後,還剩:
[D(1 + R)2 − P1](1 + R) − P2 = D(1 + R)2 − P1(1 + R) − P2
第三期償還後,還剩:
[D(1 + R)2 − P1(1 + R) − P2](1 + R) − P3 = D(1 + R)3 − P1(1 + R)2 − P2(1 + R) − P3
由此類推,第n期償還Pn後,便還清所有款項即:
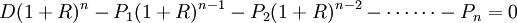
即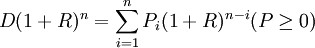
- 3.應用(等額方式)
某用戶從21歲開始,每年存入銀行退休保險金a元,如果平均每年利息為R,直到60歲退休為止,從61歲開始每年從銀行提取2萬元,預計能連續支付40年,則該用戶在工作期間,每年存入銀行的錢款數為多少?解:第一年(21歲時)存入a元,當此用戶61歲去取時,a元就會升值到
a(1 + R)40
第二年又存入a元,最終升值到a(1 + R)39
由此得出數列an
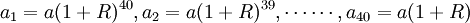
則有![S_{40}=a_1+a_2+\cdots\cdots+a_{40}=a(1+R)[(1+R)^{39}+(1+R)^{38}+\cdots\cdots+1]=a(1+R)\frac{(1+R)^{40}-1}{R}](/w/images/math/4/d/7/4d7c20e5c3ca9287c9e1bfced16c02da.png)
此用戶61歲開始逐年提取退休保險金。
第一年取2萬元,那麼還剩(S40 − 2)萬元;
第二年取2萬元,因為前一年取剩的錢還有利息,所以第二年取剩的錢就為(S40 − 2)(1 + R) − 2
由此可得數列:bn
b1 = S40 − 2
b2 = (S40 − 2)(1 + R) − 2
b3 = (S40 − 2)(1 + R)2 − 2(1 + R) − 2
…………
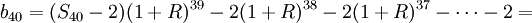
![S_{40}(1+R)^{39}-2(1+R)^{38}-2(1+R)^{37}-\cdots-2=S_{40}(1+R)^{39}-2[(1+R)^{38}+(1+R)^{37}+\cdots+1]=s_{40}(1+R)^{39}-\frac{(1+R)^{40}-1}{R}=0](/w/images/math/6/1/6/6163224c363bb51ebb2ef54cd3da0d0b.png)
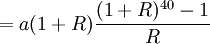 ①
①
又![S_{40}(1+R)^{39}=\frac{2[(1+R)^{4}-1]}{R}](/w/images/math/3/f/6/3f6a527d40ffe7d7b9f8296ef56f41e6.png) ②
②
由①②得![a(1+R)\frac{(1+R)^{40}-1}{R}(1+R)^{39}=\frac{2[(1+R)^{4}-1]}{R}](/w/images/math/a/c/c/acc1c9c73a2597386b1d729304b6f670.png)
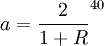
故每年應向銀行存入元才能保證退休後每年能取2萬元錢而取整整40年。
延期付款與分期付款的區別[2]
延期付款雖與分期付款類似,但兩者還是有下列重大區別。
(1)貨款支付時問不同。採用分期付款,其貨款是在交貨時付清或基本付清;而採用延期付款時,大部分貨款是在交貨後一個相當長的時間內分期攤付。
(2)貨物所有權轉移時間不同。採用分期付款時,只要付清最後一筆貨款,貨物所有權即行轉移;而採用延期付款時,貨物所有權一般在交貨時即轉移。
(3)是否要求買方向賣方支付利息問題上也有所不同。採用分期付款,買方沒有利用賣方的資金,因而不存在利息問題;而採用延期付款時,買方利用了賣方的資金需要向賣方支付利息。
在採用分期付款或延期付款時往往將匯付、托收和信用證付款三者結合使用,即主要貨款採取信用證付款方式,少量貨款或貨款尾數則採用匯付或托收方式。
評論(共5條)
向工商銀行貸款50000元,10年還清月利息是4.2‰.這道題解法好像錯了,10年也就是120個月,而您用的是160,是不是錯了?
謝謝指正,原文已重新添加了新案例和內容,希望對您有幫助哦~
MBA智庫百科是可以自由參與的百科,如有發現錯誤和不足,您也可以參與修改編輯,只要通過網頁右上角的創建新帳號,創建用戶名後即可參與,期待您的加入哦!~
貨款支付時問不同。採用分期付款,其貨款是在交貨時付清或基本付清;而採用延期付款時,大部分貨款是在交貨後一個相當長的時間內分期攤付。 錯誤了吧。
主要貨款採取信用證付款方式,少量貨款或貨款尾數則採用匯付或托收方式。








向工商銀行貸款50000元,10年還清月利息是4.2‰.這道題解法好像錯了,10年也就是120個月,而您用的是160,是不是錯了?