單純形法
出自 MBA智库百科(https://wiki.mbalib.com/)
單純形法(Simplex Method)
目錄 |
單純形法的提出及依據[1]
單純形法是美國數學家George Dantzig於1947年首先提出的。
其理論根據是:線性規劃問題的可行域是n維向量空間Rn中的多面凸集,其最優值如果存在必在該凸集的某頂點處達到,該頂點所對應的可行解稱為基本可行解。
單純形法是一種多變數函數的尋優方法,其主要思想是先找一個基本可行解,判斷是否為最優解,如果不是則找另外一個解,再進行判定,如此迭代運算,直至找到最優解或者判定其無界。
單純形法是一種直接、快速的搜索最小值方法,其優點是對目標函數的解析性沒有要求,收斂速度快,適用面較廣。
單純形法的一般解題步驟可歸納如下:
1.把線性規劃問題的約束方程組表達成典範型方程組,找出基本可行解作為初始基本可行解。
2.若基本可行解不存在,即約束條件有矛盾,則問題無解。
3.若基本可行解存在,從初始基本可行解作為起點,根據最優性條件和可行性條件,引入非基變數取代某一基變數,找出目標函數值更優的另一基本可行解。
4.按步驟3進行迭代,直到對應檢驗數滿足最優性條件(這時目標函數值不能再改善),即得到問題的最優解。
5.若迭代過程中發現問題的目標函數值無界,則終止迭代。
改進的單純形法[2]
原單純形法不是很經濟的演算法。1953年美國數學家G.B.丹齊克為了改進單純形法每次迭代中積累起來的進位誤差,提出改進單純形法。其基本步驟和單純形法大致相同,主要區別是在逐次迭代中不再以高斯消去法為基礎,而是由舊基陣的逆去直接計算新基陣的逆,再由此確定檢驗數。這樣做可以減少迭代中的累積誤差,提高計算精度,同時也減少了在電腦上的存儲量。
改進的單純形法是在單純形操作中引入變異操作,以此來增強全局搜索能力。具體做法是:
首先,進行基本單純形法操作,快速得到局部極小值,再對極小值點在取值範圍內進行變異操作,並重新進行基本單純形法操作,直到得到最優解為止。該演算法的計算步驟如下:
(1)選取初始單純形,初始步長L,最大變異次數mmax,計數器m=0;
(2)進行基本單純形操作,找到一個極值點X1;
(3)以極值點置作新的頂點,再選取初始單純形,併進行新一輪的單純形操作,得到新的極值點,兩極值點對應的目標函數為R1,R2;
(4)若R1 > R2,R1 = R2,X1 = X2,
代入: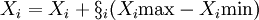 (i=1,2,…,t)(1)
(i=1,2,…,t)(1)
式中,Ximax、Ximin為參數X_i的上、下限;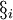 為0到1之間的隨機數。
為0到1之間的隨機數。
(5)若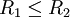 ,對進行變異操作,計數器m=m+1:
,對進行變異操作,計數器m=m+1:
(6)若計數器m < mmax,轉(1),否則輸出結果X1。
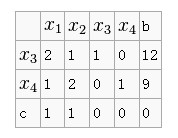
即求max:x1+x2,列單純形表(即矩陣):
原理1,根據方程組消元法對矩陣進行行變換,變換後約束條件等價不變。如以上實例。
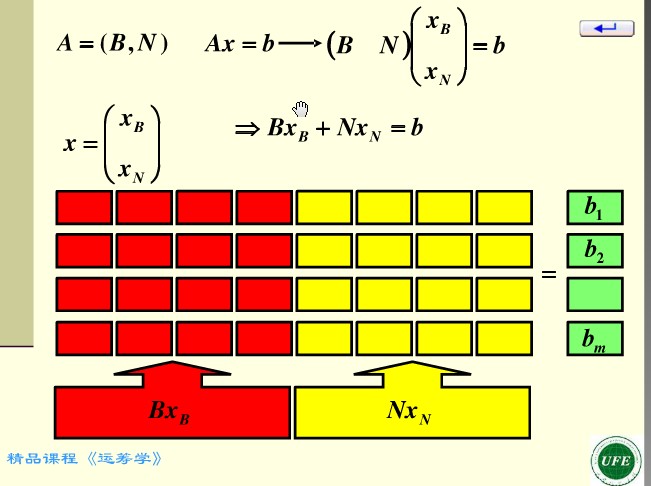
原理2,令非基變數為0,此時基變數的取值滿足約束條件。單純形法正是通過消元法交換基變數和非基變數,令非基變數為0,以求達到目標函數最優值的基變數組合。基變數即為繫數為1,0的變數。 圖解如下: 初始,將非基變數和基變數分為各自兩部分,
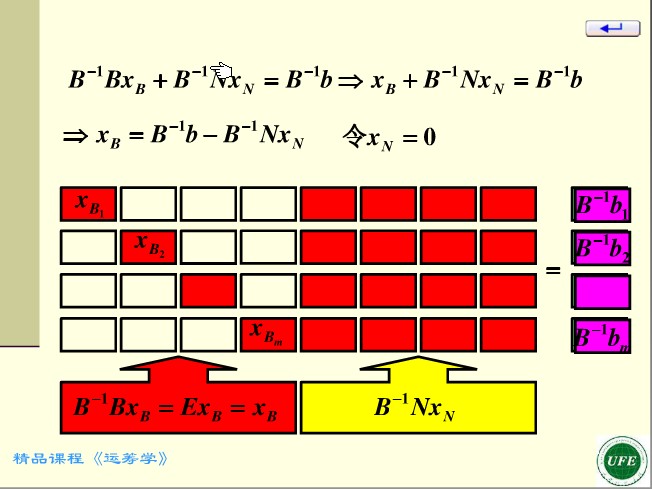
對矩陣進行行變換,
如圖所示,令非基變數為0,此時基變數的取值仍滿足約束條件。基變數的取值為![]()
原理3,對實例中c行的變換的解釋: 將基變數用非基變數表示如下圖,
x1到xm即基變數。
顯然當![]() 的累加值小於0時,令非基變數為0則Z(實例中x1+x2)達到最大。
的累加值小於0時,令非基變數為0則Z(實例中x1+x2)達到最大。
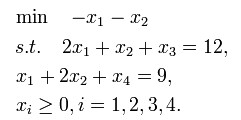



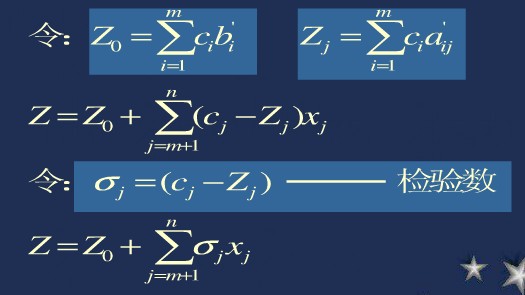








很具體,很實用