輻角原理
出自 MBA智库百科(https://wiki.mbalib.com/)
輻角原理(Principle of argument)
目錄 |
在復分析中,輻角原理是指如果 f(z) 是在某個圍道 C 上以及內部一個全純函數,且 f 在 C 上沒有零點或極點,則下列公式成立
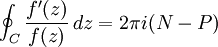
這裡 N 與 P 分別表示 f(z) 在圍道 C 內部的零點與極點個數,每個零點計重數,極點計階數。定理的陳述假設圍道 C 是簡單的,即沒有自交,以及它是逆時針方向定向的。
更一般地,假設 C 是一條曲線,逆時針方向定向,在復平面中一個開集 Ω 中可縮為一點。對每個 z ∈ Ω,令 n(C,z) 是 C 繞點 z 的卷繞數。則
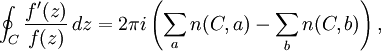
這裡第一個求和對 f 所有零點 a 進行並計重數,第二個求和在 f 的所有極點 b 上進行。
設 zN 是 f 的一個零點。我們可將 f 寫成 f(z) = (z −zN)kg(z) 這裡 k 是零點的重數,從而
g(zN) ≠ 0。我們有
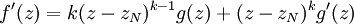
以及
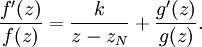
因 g(zN) ≠ 0,故 g′(z)/g(z)在
zN 沒有奇點,從而在 zN 解析,這意味著
f′(z)/f(z) 在 zN 的留數是 k。
設 zP 是 f 的一個極點。我們可寫成 f(z) = (z −zP)−mh(z) 這裡 m 是極點的階數,從而
h(zP) ≠ 0。則
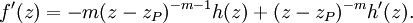
以及
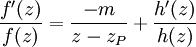
如上。故 h′(z)/h(z) 在 zP 沒有奇點,因為
h(zP) ≠ 0 從而在 zP 解析。我們發現
f′(z)/f(z) 在 zP 的留數是 −m。
將它們放在一起,f 的每個 k 重零點 zN 產生
f′(z)/f(z) 的一個留數為 k 的單極點,而 f 的每個 m 階極點 zP 產生 f′(z)/f(z) 的一個留數為 −m 的單極點(這裡一個單極點指一階極點)。另外,可以證明 f′(z)/f(z) 沒有其它極點,從而沒有其它留數。
由留數定理我們有關於 C 的積分是 2πi 與這些留數之和的乘積。總之,每個零點 zN 的 k 之和是計重數的零點個數,對極點類似,故我們得到了欲證之結論。
按照弗蘭克•史密西斯一書(Cauchy and the Creation of Complex Function Theory, Cambridge University Press, 1997)的說法,在奧古斯丁•路易•柯西從法國到都靈(當時皮德蒙特-薩丁尼亞王國的首都)的自我放逐途中,柯西於1831年11月2日提出了和上面類似的一個定理(見177頁)。但是根據此書,只提到了零點,沒有極點。柯西的這個定理在許多年後的1974年才以手寫本發表,故很難閱讀。柯西逝世兩年前的1855年發表的一篇論文中,零點與極點都討論了。定理 1 只涉及了零點。柯西1855年論文中的定理 2 說“一個單復變數函數 Z 的對數計量(compteurs logarithmiques,相當於現代教材中的對數留數)等於 Z 與 1/Z 根的個數之差(相當於現代教材中的函數 Z 的零點與極點)。從而現代“輻角原理”可在1855年柯西論文中作為一個定理髮現。
假設 C 是一個以原點為中心的閉圍道,通過考慮 f(z) 關於原點的卷繞數可得出一些推論。我們看到 f′(z)/f(z) 在 C 上的積分是 log f(z) 值的變化。因為 C 是閉的我們只需考慮 i arg f(z) 在 C 上的變化,它將是 2πi 的某個整數倍因為 C 是閉的(但可能繞原點捲多圈)。但從輻角原理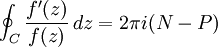
約去因數 2πi,我們得到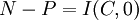
這裡 I(C,0) 表示 f 在 C 上關於 0 點卷繞數。
一個推論是更廣泛的定理,在同樣的假設下,如果 g 是 Ω 中一個解析函數,則
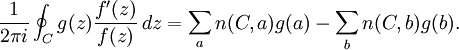
例如,如果 f 是以一個簡單圍道 C 內部 z1, ..., zp 為零點的多項式,以及g(z) = zk,則
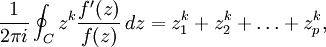
是 f 的根的冪和對稱函數。
另一個推論是如果我們計算復積分:
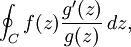
對一個合適的 g 與 f,我們有尼爾斯•阿貝爾公式:
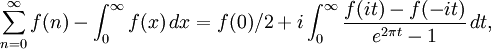
這給出了一個離散和式與它的積分之間的關係。
反饋控制理論的現代書籍中頻繁用到輻角原理,將其作為奈奎斯特穩定性判據的理論基礎。哈里•奈奎斯特1932年原理的論文(H. Nyquist, "Regeneration theory", Bell System Technical Journal, vol. 11, pp. 126-147, 1932)用一種相當笨拙與原始的方法得出奈奎斯特穩定性判據。在這篇論文中,奈奎斯特完全沒有提到柯西的名字。後來,Leroy MacColl (Fundamental theory of servomechanisms, 1945) 與 Hendrik Bode (Network analysis and feedback amplifier design, 1945) 都從輻角原理得到了奈奎斯特穩定性判據。MacColl (Bell Laboratories) 將輻角原理稱為柯西定理。這樣輻角原理在純粹數學與控制工程學中都有重大影響。現在,輻角原理可在復分析或控制工程學的現代教材中都可以找到。







