路徑覆蓋
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
路徑覆蓋是指選取足夠多的測試數據,使程式的每條可能路徑都至少執行一次(如果程式圖中有環,則要求每個環至少經過一次)。路徑覆蓋是覆蓋率最高的一種覆蓋技術。
路徑覆蓋要求設計足夠多的測試用例,在白盒測試法中,覆蓋程度最高的就是路徑覆蓋,因為其覆蓋程式中所有可能的路徑。對於比較簡單的小程式來說,實現路徑覆蓋是可能的,但是如果程式中出現了多個判斷和多個迴圈,可能的路徑數目將會急劇增長,以致實現路徑覆蓋是幾乎不可能的。
路徑覆蓋率的公式:路徑覆蓋率=被執行到的路徑數/程式中總的路徑數。
1、將程式流程圖轉換成控制流圖;
2、經過語法分析求的路徑表達式;
3、生成路徑圖;
4、進行路徑編碼;
5、經過解碼得到執行的路徑;
6、通過路徑枚舉產生特定路徑測試用例;
7、修正的條件判斷覆蓋率。
完全路徑覆蓋測試方法[1]
雖然路徑覆蓋是覆蓋率最高的,但是,簡單的程式路徑數量很少,而複雜的程式路徑數量巨大,要實現路徑覆蓋幾乎不可能,即測試量過大;另外,即使滿足了程式結構一般意義上的路徑覆蓋,仍然不能保證被測程式的正確性,即測試不足。如果要求測試更加充分,則要求增加更多的測試用例來提高覆蓋率,測試量會更大,於是,測試中就產生了測試量過大和測試不足這一對矛盾。
對於獨立路徑數的計算可以採用下麵的方法:
第一步,從流圖中找出程式所有的必經節點(流圖中任何獨立路徑都必定經過的節點叫做必經節點),記作IV(i),其中i為整數且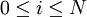 。
。
第二步,從流圖中找出從必經節點N(i)到必經節點N(i+1)的獨立路徑數W(i),其中i為整數且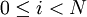 。
。
第三步,重覆上一步,直到程式結尾。
第四步,根據乘法法則,獨立路徑數= W(i),其中i為整數且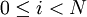 ,即獨立路徑數=W(0) * W(1) * ⋯ * W(N一1)。
,即獨立路徑數=W(0) * W(1) * ⋯ * W(N一1)。
完全路徑是指所有獨立路徑的集合,非完全路徑就是所有獨立路徑集合的真子集。由於程式中可能會包含有多個條件的判定,所以程式流程圖可能包含有隱含路徑,從而有程式流圖轉換成的對應流圖可能包含有隱藏路徑。如圖1、圖2所示。
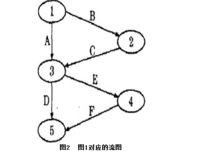
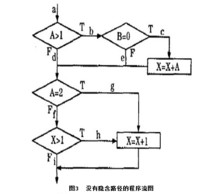
消除隱含路徑的辦法就是將含有多個條件的判定分為多個判定。即把圖1的程式流圖轉換成如圖3所示,圖4是其對應的流圖。
圖4中,節點1,4,7為必經節點,W(0)=3,W(1)=3,所以獨立路徑數=3*3=9。由此,要達到完全路徑覆蓋就需要設計9個測試用例,從而使得測試量更加龐大。根據線性代碼序列與跳轉的測試覆蓋準則,將程式在必經節點處割斷,分別對每一段程式進行完全路徑覆蓋的充分測試。對於被割斷的程式片斷,由於沒有參數人口,可以在程式片斷的開頭增加代碼對參數進行初始化。從而達到完全測試,緩解測試量過大與測試不足的矛盾。
 |  |  | 
|
總結完全路徑覆蓋的具體步驟如下:
1、將判定語句的條件進行分離,細化程式流程圖,使其不含隱含路徑。
2、根據程式流程圖畫出流圖,找出必經節點,必經節點數為N。
3、將程式流程圖在必經節點處割斷,將整個程式分解為N+1個程式片斷。
4、找出程式片斷i的完全路徑,為程式片斷i的每條獨立路徑設計用例,其中: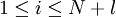 。
。
5、結合所設計的測試用例,將程式片斷i的參數初始化,其中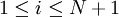 。
。
6、將測試用例付諸測試,重覆第四步至第六步,直到i=N+1。







