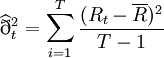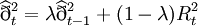變異數－共變異數法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　變異數－共變異數法也稱為相關法（Correlation Method），參數（Parametric）法、線型（Linear）法或一階常態（Delta－Normal）法 。

　　主要的假設就是個別資產報酬率符合聯合常態分配，而且具有序列獨立的特性。

　　由這些資產所構成的線性組合資產，一定會服從常態分配，藉由常態分配的性質再來估計出給定評估期間與信賴機率水平下的風險值。

　　常態分配的假設使得變異數－共變異數法可以快速的算出風險值。

　　建構投資組合中個別資產於未來評估期間的損益（或報酬）分配；

　　納入個別資產間的相關性，進而建構整個投資組合於未來評估期間的損益（或報酬）分配。

　　傳統上通常利用移動平均的觀念來估算變異數，並且可進一步分為等權移動平均與指數加權移動平均兩種方式。

　　相等（簡單）加權移動平均法

　　指數加權移動平均法