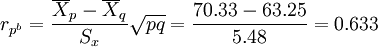點雙列相關

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

(重定向自点二列相关)

點雙列相關(Point Biserial Correlation)

什麼是點雙列相關^[1]

　　點雙列相關又稱點二列相關，適用於兩列變數中一列是來自正態總體的等距或等比數據，另一列是二分稱名變數，即按事物的某一性質只能分為兩類相互獨立的變數，譬如，男與女，生與死，已婚與未婚等。

[編輯]

點雙列相關的計算方法^[2]

　　點雙列相關的計算公式如下：

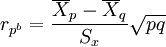
　　 $r_{p^b}=\frac{\overline{X}_p-\overline{X}_q}{S_x}\sqrt{pq}$

　　其中，p——二分稱名變數中取某一值的變數比例；

　　q——二分稱名變數中取另一值的變數比例；

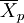　　 $\overline{X}_p$ ——等距(等比)變數中與P對應那部分數據的平均值；

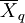　　 $\overline{X}_q$ ——等距(等比)變數中與q對應那部分數據的平均值；

　　 $S x$ ——全部等距(等比)變數的標準差。

　　點雙列相關在教育研究中常作為選擇題的區分度指標。

　　例：某次測驗中10名考生的一道單項選擇題得分和其捲面總分如下表所示，試求該單項選擇題的區分度。

考生	A	B	C	D	E	F	G	H	I	J
選擇題得分	1	0	1	1	0	1	1	0	1	O
捲面總分	76	58	74	67	65	68	71	69	66	61

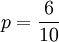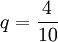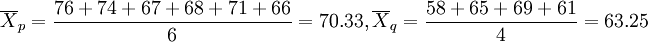　　解：此題中，單選題的得分只有1和0兩種，是二分稱名變數，其捲面得分為等比數據，且來自正態總體，其區分度可以用點雙列相關係數來表示。先求各個相關的參數，已知n=10，求得捲面總分的標準差 $S x = 5.48$ ，該選擇題得分為1的考生比例 $p=\frac{6}{10}$ ，選擇題得分為0的考生比例 $q=\frac{4}{10}$ ， $\overline{X}_p=\frac{76+74+67+68+71+66}{6}=70.33,\overline{X}_q=\frac{58+65+69+61}{4}=63.25$ 。