本福特法則
出自 MBA智库百科(https://wiki.mbalib.com/)
本福特法則(Benford's law)
目錄 |
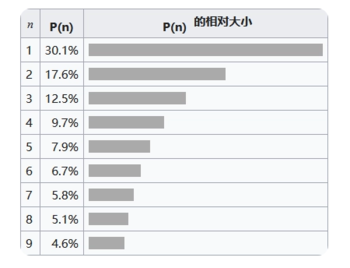
本福特法則,也稱“本福特定律”,以提出者物理學家本福特的名字命名,指的是一堆從實際生活得出的數據中,以1為首位數字的數的出現機率約為總數的三成,接近期望值1/9的3倍,推廣來說,越大的數字,以它為首幾位的數出現的機率就越低;精確地數學表述為:在b進位制中,以數n起頭的數出現的機率為logb(n + 1) − logb(n)[1]。
本福特法則的適用範圍[1]
本福特定律產生的根源,就在於指數增長。而指數增長的形式在自然界是十分普遍的,只要一個變數的增長率和他的大小成正比,結果就會是指數增長。比如說人類科技發展的速度大致和已有的科技成果成正比,所以人類的科技發展就是個指數增長;人口增長率會和已存在人口數成正比,因此沒有資源限制的人口增長也是指數增長。指數增長是自然中極為普遍的一種變化規律,而這種變化規律可以直接導致本福特定律。
這個定律是一個非常神奇的定律,它的適用範圍異常的廣泛,幾乎所有日常生活中沒有人為規則的統計數據都滿足這個定律。比如說世界各國人口數量、各國國土面積、賬本、物理化學常數、數學物理課本後面的答案、放射性半衰期等等數據居然都符合本福特定律。值得一提的是,科學家還發現,統計物理的三個重要分佈,Boltzmann-Gibbs分佈,Bose-Einstein分佈,Fermi-Dirac分佈,也基本上滿足Benford定律。
使用本福特法則必須滿足的條件
第一,這些數據必須跨度足夠大,必須橫跨好幾個數量級才能產生這個結果。數據樣本需要儘可能的多,至少要在3000個以上;其次,數據樣本跨度要大,比如人的身高就不滿足“本福特定律”,因為大多數人身高在1米至2米這一區間;
第二,有人為規則的數據就不滿足次定律,比如說手機號碼、身份證號、發票編號等數據,明顯不滿足這種對數分佈律。也就是說,本福特定律正是沒有任何限制才顯露出來的定律,越是對數據的產生有人為限制,越是不滿足該定律。第三,數據不能經過人為修飾,隨便人為修改的數據一般就不滿足本福特定律了,比如當年著名的安然公司造假案,他們的賬本就沒有滿足本福特定律,因此這個神秘的定律甚至可以用來判別是否財務造假。
統計國家地區人口數
李永樂老師統計2000年世界上235個國家和地區人口數,以及首位分別是1-9的占比數據。
然後,將實際頻率和本福特法則預測概率合在一起圖解。我們們會發現,兩者很接近。
本福特法則揭示的分佈現象很普遍。多數沒有人為干預的統計數據,例如,世界各國人口數量、各國國土面積、賬本、物理化學常數、數學物理課本後面的答案、放射性半衰期等,都滿足本福特法則。
值得一提的是,科學家還發現,統計物理的3個重要分佈,波茲曼-吉布斯分佈,玻色-愛因斯坦分佈,費米-狄拉克分佈,也基本滿足本福特法則。
如此普遍,以至於現在科學家還在持續研究本福特法則。讀友們如果有興趣,也可以挑選一些領域,來考察各種數據的首位數分佈。
鑒別造假[2]
在數據造假領域,不難理解,造假者人為篡改數據,如果不夠完美,就很容易與本福特法則預測數據產生偏差。
我們來看一個案例。2001年,美國最大能源交易商、年收入破千億美元的安然公司宣佈破產,同時傳出公司財務造假的傳聞。
於是,有人用本福特法則對安然公司公佈的財務報表進行檢驗。
發現數字1、8、9頻率相比本福特法則預測明顯偏大,數字2、3、4、5、7又明顯偏小。這意味著,安然公司造假可能性較大。
經過調查,美國司法部最終認定安然公司財務造假。安然公司CEO傑弗里·斯基林被判刑24年並罰款4500萬美元,財務欺詐策劃者費斯托被判6年徒刑並罰款2380萬美元。
安然醜聞發生後,有89年曆史位列全球第五大會計師事務所的安達信,因幫助安然公司造假,被判處妨礙司法公正罪後宣告破產。
目前,本福特法則已經成為會計師們判斷銷售數據、財務報表等數據是否造假的依據之一,甚至還有人使用本福特法則,來檢驗選舉中是否存在舞弊現象。
- ↑ 1.0 1.1 神秘的本福特定律.果殼.2010-10-31
- ↑ 張龍逸. 對本福特法則的實證檢驗——以國內全體上市公司的財務報表為例[J]. 中國集體經濟, 2020(28):3.