無名氏定理
出自 MBA智库百科(https://wiki.mbalib.com/)
無名氏定理(Folk Theorem),也稱佚名定理、大眾定理、俗定理
無名氏定理(Folk Theorem)即在重覆博弈中,只要博弈人具有足夠的耐心(貼現因數足夠大),那麼在滿足博弈人個人理性約束的前提下,博弈人之間就總有多種可能達成合作均衡。存在無窮多對有限自動機策略,可以成為無限重覆博弈的平衡點,並同時實現雙方的合作。無名氏定理之所以得名,是由於重覆博弈促進合作的思想,早就有很多人提出,以致無法追溯到其原創者,於是以“無名氏”命名之。
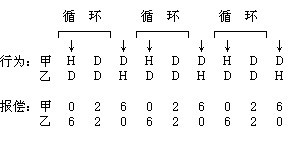
我們知道,單憑理性計算,有限次重覆博弈,是解決個體理性與集體理性之間矛盾的。在無限重覆博弈中,行為規則可以用自動機來代表,於是不同行為規則的相爭,便成了機器與機器的角鬥。假設甲和乙玩無限重覆的囚犯博弈。甲相信《美德的起源》一書作者的教導,認定仁厚忠恕既高尚又有效,於是以它為策略。乙信奉理性流氓主義,崇尚實力和實利,於是以流氓主義為策略。這樣,二人間的博弈,就可以看作恕道機器與流氓機器的爭鬥。我們可以推演出各個回合雙方的行為如下:第一回合,甲仁厚玩合作H,乙宰客玩欺騙D;第二回合,甲報複玩欺騙D,乙仍然宰客玩欺騙D;第三回合,甲仍報複玩欺騙D,乙發現甲並非傻客,於是玩合作H;第四回合,甲原諒乙,玩合作H;乙卻因甲上次不合作,回頭玩欺騙D宰客;……如此等等。整個結果序列如下圖所示:
請註意,此序列呈現一個有趣的規律:就是每三個一組,不斷迴圈重覆。於是我們很容易算出,博弈各方平均每個回合的報償有多少,只要取相繼三個回合,作個簡單平均就夠了。甲得到(0+2+6)/3= 2.67,乙得到(6+2+0)/3= 2.67 。顯然,兩者平分秋色,不相上下,誰也不比誰差,誰也不比誰強。
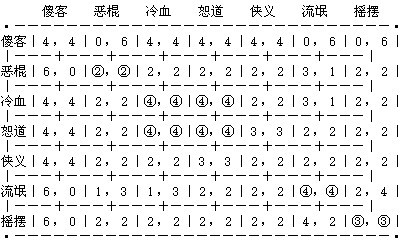
這種迴圈重覆並不是特例。可以證明,有限自動機玩無限重覆博弈,其結果最終都會變成迴圈重覆序列。於是,利用類似的辦法,我們可以針對下表中列出的七種策略,算出每一對策略相博所產生的的平均報償。這些報償可以寫成一個7×7博弈矩陣,如下表所示(其中一些略去了小數,這不影響下麵的討論):
上面這個表裡面,有帶圈數字的格子都是平衡點。比如,乙玩惡棍策略時,甲無論玩什麼,都不比當惡棍帶來的好處更多,頂多不致受損而已。因此,甲乙雙方都當惡棍,次次都玩欺騙,便是重覆囚犯博弈的平衡點之一,此時各方的報償與一次性博弈相同,都是2。
觀察一下上面這個表,我們會發現它有多個平衡點。非重覆博弈中的均衡點,惡棍對惡棍,雙方永遠玩欺騙,仍然是無限重覆博弈的均衡點。無條件合作的傻客策略,仍然不是重覆博弈的均衡點,理性的人,決不會當傻客。更重要的是,重覆博弈引進了許多新的平衡點,其中有不少平衡點,可以實現合作報償(4,4)。這包括恕道策略對恕道策略,恕道策略對冷血策略,冷血策略對冷血策略,流氓策略對流氓策略等,都可以維持雙方的合作。以流氓對流氓為例:第一回合,雙方耍流氓互宰,發現對方不是好惹的之後,雙方轉入合作心態,此後一直維持合作,這樣無限次重覆,其平均報償都是4。事實上,存在無窮多對有限自動機策略,可以成為無限重覆博弈的平衡點,並同時實現雙方的合作。這就是有名的“大眾定理(Folk Theorem)”,又譯作“無名氏定理”。它之得名,是由於重覆博弈促進合作的思想,早就有很多人提出,以致無法追溯到其原創者,於是以“無名氏”名之。
大眾定理說明瞭行為規則的多樣性:有無窮多種行為規則可以支持合作行為。在正常的平衡狀態中,可觀察到的行為可以完全相同的,此即博弈雙方相互合作,不玩欺騙。但其背後的行為規則卻可能大不相同合作,可以是由於雙方都信奉仁厚的恕道主義,也可能是因為雙方都是理性;流氓,還可能是因為雙方都一冷血報複作威脅。這些行為規則上的區別,在正常的平衡狀態中,是看不出來的,只有在非正常情況下,或在與外人的交往中,才會表現出來。 為說明此點,設想有兩個相互隔離的社會:一個形成了理性流氓式的行為規則,一個形成仁厚恕道的行為規則,他們各自內部都能維持相互合作,這形成了社會的正常狀態。外人但憑觀察這兩個社會中人們的正常行為,看不出他們有什麼區別。現在假設兩個社會打破隔離,相互接觸,會產生甚麼情況?兩套行為規則間會出現激烈的衝突!
初次接觸,流氓主義者將把對方當傻客,大宰其客。恕道主義者假設對方是好人,選擇合作,只是在吃了虧之後,才以回宰其客相回報。流氓主義者見對方回宰,以為對方也是跟自己一樣的流氓,於是轉向合作心態,同時預期對方也選擇合作。但恕道主義者根據“以直報怨”的原則,仍然以宰客回報對方上次的欺騙。流氓主義者一看對方不合作,怒從心起,於是報之以宰客,如此迴圈往複,雙方永遠無法達成合作。
行為規則的衝突,類似於人文學科里常說的文化衝突。由於行為規則反映了人們對各自行為的穩定預期,一些博弈論者把不同的行為規則解釋為不同的文化信仰,應當是不無道理的。重覆博弈理論,為我們科學理解許多文化現象,打開了大門。








聽不懂