感應度繫數

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

感應度繫數概述

　　感應度繫數是指國民經濟各部門每增加一個單位最終使用時，某一部門由此而受到的需求感應程度，也就是需要該部門為其他部門生產而提供的產出量。繫數大說明該部門對經濟發展的需求感應程度強，反之，則表示對經濟發展需求感應程度弱。

[編輯]

感應度繫數的計算^[1]

　　(1)

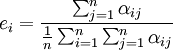
　　 $e_i=\frac{\sum_{j=1}^n \alpha_{ij}}{\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^n\alpha_{ij}}$

　　(2)

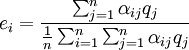
　　 $e_i=\frac{\sum_{j=1}^n\alpha_{ij}q_j}{\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^n\alpha_{ij}q_j}$

　　(3)

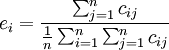
　　 $e_i=\frac{\sum_{j=1}^nc_{ij}}{\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^nc_{ij}}$

　　(4)

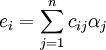
　　 $e_i=\sum_{j=1}^nc_{ij}\alpha_j$

　　(5)

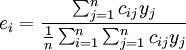
　　 $e_i=\frac{\sum_{j=1}^nc_{ij}y_j}{\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^nc_{ij}y_j}$

　　(6)

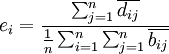
　　 $e_i=\frac{\sum_{j=1}^n\overline{d_{ij}}}{\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^n\overline{b_{ij}}}$

　　(7)

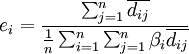
　　 $e_i=\frac{\sum_{j=1}^n\overline{d_{ij}}}{\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^n\beta_i\overline{d_{ij}}}$

　　(8)

　　 $e_i=\sum_{j=1}^n\beta_i\overline{d_{ij}}$

　　上述公式中 $α i j$ 為直接消耗繫數; $q j$ 為j部門的總產出; $y j$ 為j部門的最終產出為;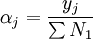 $\alpha_j=\frac{y_j}{\sum{N_1}}$ 為j部門的最終產出占最終產出總量的比例,即最終產出結構繫數; $c i j$ 為完全需求繫數; 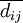$\overline{d_{ij}}$ 為完全供給繫數; 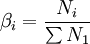$\beta_i=\frac{N_i}{\sum{N_1}}$ 為i部門最初投入占最初投入總量的比例,即最初投入結構繫數。

[編輯]

參考文獻

↑ 王燕，宋輝.影響力繫數和感應度繫數計算方法的探析.河北大學經濟學院.價值工程2007年4期

[編輯]

本条目由以下用户参与贡献

Cabbage,鲈鱼.

頁面分類: 統計指標

評論(共2條)

提示:評論內容為網友針對條目"感應度繫數"展開的討論，與本站觀點立場無關。

Soyoyo0712 (討論 | 貢獻) 在 2011年1月24日 20:43 發表

公式錯誤，這個是影響力繫數的求解。改不來，囧。。。

回複評論

鲈鱼 (討論 | 貢獻) 在 2011年1月25日 10:39 發表

Soyoyo0712 (討論 | 貢獻) 在 2011年1月24日 20:43 發表

公式錯誤，這個是影響力繫數的求解。改不來，囧。。。

謝謝指正！~已對公式進行了修改~

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

感應度繫數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

感應度繫數概述

感應度繫數的計算^[1]

參考文獻

相關條目

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共2條)

導航

意见反馈

查看

工具▼

感應度繫數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

感應度繫數概述

感應度繫數的計算[1]

參考文獻

相關條目

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共2條)

導航

意见反馈

感應度繫數的計算^[1]