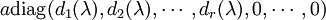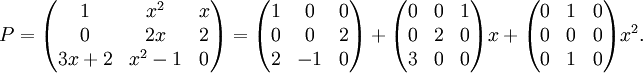多項式矩陣
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
多項式矩陣是指數學中矩陣論里繫數是多項式的方塊矩陣。
給定自然數和繫數環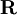 ,一個階多項式矩陣為如下形式:
,一個階多項式矩陣為如下形式:
![A(\lambda)=[a_{i,j}(\lambda)]_{1\le i,j\le n}](/w/images/math/7/9/6/7961729ce5763d6063b511cc4502eac2.png) ,
, ,
,![a_{i,j}(\lambda)=\sum_{k=0}^{d_{i,j}}a_{i,j,k}\lambda^k\in R[\lambda]](/w/images/math/c/0/3/c03e985a946a9ac68ad02842cf11b1c7.png) ,
,
其中di,j是每個多項式ai,j(λ)的次數。
如果設其中最大的為d:
- d = maxdi,j,
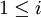 ,
, 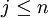
那麼多項式矩陣也可以表達為:
![A=\sum_{k=0}^d \lambda^k[a_{i,j,k}]=\sum_{k=0}^d A(K)\lambda^k](/w/images/math/8/8/a/88a61eebccc47bd3aca5dd3a94c4c4f7.png) ,
,
其中約定當k > di,j時,ai,j,k = 0.
由於多項式矩陣也能被表達為以(數值)矩陣為繫數的多項式,所以也被稱為矩陣繫數多項式。如果最高次繫數矩陣A(d)的行列式不為零,則稱多項式矩陣為為正則多項式矩陣。所有階多項式矩陣的集合記為![\mathcal{M}_{n}(\mathbf{R}\left[\lambda\right])](/w/images/math/2/7/9/279faf7aaa9e903e6fe99389a7097998.png) 或
或![\mathcal{M}_{n}(\mathbf{R})\left[\lambda\right]](/w/images/math/3/8/b/38b930b993a837799fd3dbe0b97c072c.png) 。前者表示所有以多項式為繫數的階方塊矩陣的集合,後者表示所有階方塊矩陣為繫數的多項式的集合。可以驗證兩者是同構的。
。前者表示所有以多項式為繫數的階方塊矩陣的集合,後者表示所有階方塊矩陣為繫數的多項式的集合。可以驗證兩者是同構的。
由於多項式代數和矩陣代數的結構特性,環R上的所有階多項式矩陣也構成一個代數(環論)。兩個階多項式矩陣可以互相加減、相乘,並且滿足加法交換律和乘法分配律(不滿足乘法交換律)。用與數值矩陣相同的方式可以定義多項式矩陣的初等變換、相似矩陣、等價關係(也稱為“相抵”)、矩陣的秩以及行列式。
如果繫數環是域,那麼可以證明,所有的多項式矩陣都可以矩陣對角化|對角化。任何一個矩陣的秩的多項式矩陣,都可以相抵於一個對角多項式矩陣:
其中的每個非零的對角元素di(λ)都是首一多項式,並且整除下一個對角元素di + 1(λ)。這種形式稱為多項式矩陣的史密斯標準型,所有的di(λ)被稱為原多項式矩陣的不變因數。
如果將階多項式矩陣看成以階方塊矩陣為繫數的多項式,可以通過將其中的不定元替換為一個階方塊數值矩陣,而得到一個階數值矩陣。這種操作稱為多項式矩陣的矩陣替換。由於矩陣乘法不滿足交換律,所以替換分為左替換和右替換:
- 左替換:將
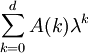 替換為
替換為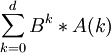 也記作
也記作
- 右替換:將
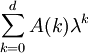 替換為
替換為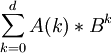 也記作
也記作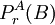
如果繫數環是域,那麼多項式矩陣之間可以做帶餘除法:如果A(λ)和B(λ)都是多項式矩陣,其中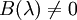 ,那麼唯一存在多項式矩陣Q(λ)和R(λ),則
A(λ) = B(λ)Q(λ) + R(λ)
R(λ)作為多項式的次數嚴格小於B(λ),或者為零。
,那麼唯一存在多項式矩陣Q(λ)和R(λ),則
A(λ) = B(λ)Q(λ) + R(λ)
R(λ)作為多項式的次數嚴格小於B(λ),或者為零。
所有的數值矩陣都是多項式矩陣,因為可以將每個元素看成一個零多項式。設繫數環為實數域,以下是一個3階多項式矩陣:
特征矩陣是多項式矩陣的一個例子。設有階數值矩陣,則特征矩陣實際上是一次多項式矩陣: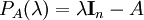 。而特征矩陣的行列式
。而特征矩陣的行列式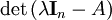 就是數值矩陣的特征多項式。
就是數值矩陣的特征多項式。