古爾丁定理
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
古爾丁定理(Goulding theorem)
目錄 |
[編輯]
古爾丁定理是指最初由古希臘的帕普斯發現,後來在16世紀保羅•高爾丁又重新發現的數學定理。
[編輯]
[編輯]
有一條平面曲線,跟它的同一個平面上有一條軸。由該平面曲線以該條軸與旋轉而產生的旋轉曲面的錶面積A,等於曲線的長度s乘以曲線的幾何中心經過的距離d1:A = sd1。
例:設環面圓管半徑為r,圓管中心到環面中心距離為R,把環面看成上面提到的曲線,其幾何中心是圓管中心。所以環面錶面積為(2πr)(2πR) = 4π2rR
若有平面連續曲線y = f(x),求x在[a,b]時,曲線以x軸旋轉所得的曲面錶面積。可考慮一小段曲線,其幾何中心便是y,曲線長度為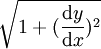 ,因此這個曲面的錶面積便是:
,因此這個曲面的錶面積便是: 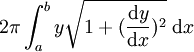 。
。
[編輯]
由平面形狀繞和它的同一個平面上的軸旋轉而產生的旋轉體的體積V,等於平面形狀面積S乘以平面形狀的幾何中心經過的距離d1的積:V = Sd1。
再考慮一般平面曲線下的面積的情況,可得旋轉體體積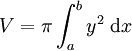 。
。







